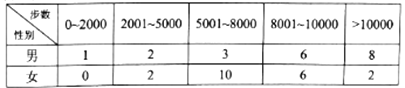
题目内容
【题目】已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜ 
）的部分图象如图所示． 
（1）求函数f（x）的解析式；
（2）求函数g（x）=f（x﹣ 
）﹣f（x+ ）的单调递增区间．
【答案】
（1）解：由图象可知，周期T=2（ 
﹣ 
）=π，∴ω= 
=2
∵点（ ，0）在函数图象上，∴Asin（2× +φ）=0
∴sin（ 
+φ）=0，∴ +φ=π+kπ，即φ=kπ+ 
，k∈z
∵0＜φ＜ 
∴φ=
∵点（0，1）在函数图象上，∴Asin =1，A=2
∴函数f（x）的解析式为f（x）=2sin（2x+ ）
（2）解：g（x）=2sin[2（x﹣ 
）+ ]﹣2sin[2（x+ ）+ ]=2sin2x﹣2sin（2x+ 
）
=2sin2x﹣2（ 
sin2x+ 
cos2x）=sin2x﹣ 
cos2x
=2sin（2x﹣ ）
由﹣ +2kπ≤2x﹣ ≤ +2kπ，k∈z
得kπ﹣ ≤x≤kπ+
∴函数g（x）=f（x﹣ ）﹣f（x+ ）的单调递增区间为[kπ﹣ ，kπ+ ]k∈z
【解析】（1）先利用函数图象求此函数的周期，从而计算得ω的值，再将点（ ，0）和（0，1）代入解析式，分别解得φ和A的值，最后写出函数解析式即可；（2）先利用三角变换公式将函数g（x）的解析式化为y=Asin（ωx+φ）型函数，再将内层函数看做整体，置于外层函数即正弦函数的单调增区间上，即可解得函数g（x）的单调增区间
练习册系列答案
相关题目
