题目内容
16.2015年春晚上,有一种旋转舞台灯,其外形呈正四棱柱,每个侧面上安装了5只不同的彩灯,每只彩灯发光的概率为$\frac{1}{2}$,若每个侧面上至少3只彩灯正常发光,则该侧面不需要维修,否则需要维修.(Ⅰ)求恰有两个侧面需要维修的概率;
(Ⅱ)设四个侧面的维修费分别为100元、100元、200元、200元,记需要维修的费用为X,求X的分布列及期望.
分析 (I)某个侧面需要维修的概率=${∁}_{5}^{2}(\frac{1}{2})^{5}$+${∁}_{5}^{1}×(\frac{1}{2})^{5}$+$(\frac{1}{2})^{5}$=$\frac{1}{2}$,可得恰有两个侧面需要维修的概率=${∁}_{4}^{2}(\frac{1}{2})^{4}$.
(II)由题意可知:X的可能取值为0,100,200,300,400,500,600.利用互斥事件与二项分布列的概率计算公式即可得出.
解答 解:(I)某个侧面需要维修的概率=${∁}_{5}^{2}(\frac{1}{2})^{5}$+${∁}_{5}^{1}×(\frac{1}{2})^{5}$+$(\frac{1}{2})^{5}$=$\frac{1}{2}$,
故恰有两个侧面需要维修的概率=${∁}_{4}^{2}(\frac{1}{2})^{4}$=$\frac{3}{8}$.
(II)由题意可知:X的可能取值为0,100,200,300,400,500,600.
其分布列为:
| X | 0 | 100 | 200 | 300 | 400 | 500 | 600 |
| P | $\frac{1}{16}$ | $\frac{1}{8}$ | $\frac{3}{16}$ | $\frac{1}{4}$ | $\frac{3}{16}$ | $\frac{1}{8}$ | $\frac{1}{16}$ |
点评 本题考查了互斥事件与二项分布列的概率计算公式、组合计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.函数$f(x)=\frac{2}{x}$的单调递减区间为( )
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (0,+∞) |
4.一个半径为$\sqrt{6}$的球的内接正四棱柱的高为4,则该正四棱柱的表面积为( )
| A. | 24 | B. | 32 | C. | 36 | D. | 40 |
1.已知角α的正弦线和余弦线长度相等,且α的终边在第三象限,则tanα等于( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{3}$ |
8.已知函数f(x)=x2+mx+n,且y=f(x+2)的图象关于y轴对称,则大小关系正确的是( )
| A. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | B. | f(1)<f($\frac{7}{2}$)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
6.已知平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,$\overrightarrow{a}=(1,1)$,$\overrightarrow{a}+3\overrightarrow{b}=(4,-2)$,则cosθ=( )
| A. | 0 | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
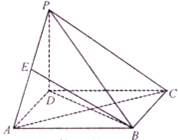 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,