题目内容
对函数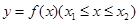 ,设点
,设点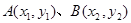 是图象上的两端点.
是图象上的两端点. 为坐标原点,且点
为坐标原点,且点 满足
满足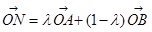 .点
.点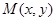 在函数
在函数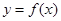 的图象上,且
的图象上,且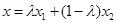 (
(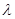 为实数),则称
为实数),则称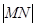 的最大值为函数的“高度”,则函数
的最大值为函数的“高度”,则函数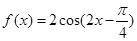 在区间
在区间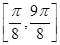 上的“高度”为 .
上的“高度”为 .
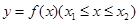 ,设点
,设点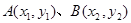 是图象上的两端点.
是图象上的两端点. 为坐标原点,且点
为坐标原点,且点 满足
满足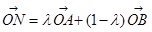 .点
.点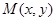 在函数
在函数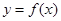 的图象上,且
的图象上,且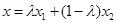 (
(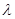 为实数),则称
为实数),则称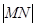 的最大值为函数的“高度”,则函数
的最大值为函数的“高度”,则函数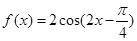 在区间
在区间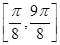 上的“高度”为 .
上的“高度”为 .4
试题分析:根据题意可知这个函数
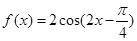 的最大值为2,而在端点值的函数值为2,同时,M,N,A,B四点共线的,因此在区间
的最大值为2,而在端点值的函数值为2,同时,M,N,A,B四点共线的,因此在区间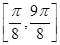 的高度就是一个周期内函数的图像上的高度,即为2+2=4,故答案为4.
的高度就是一个周期内函数的图像上的高度,即为2+2=4,故答案为4.点评:解决该试题的关键是理解向量的关系式说明而来N,A,B三点共线,同时理解函数的高度的定义,这样便于利用已知的关系式来结合三角函数的性质得到结论,属于难度试题。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
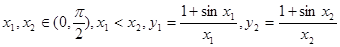 ,则( )
,则( )


 的大小不能确定
的大小不能确定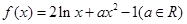
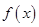 的单调区间;
的单调区间;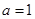 ,试分别解答以下两小题.
,试分别解答以下两小题.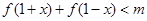 对任意的
对任意的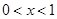 恒成立,求实数
恒成立,求实数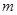 的取值范围;
的取值范围;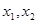 是两个不相等的正数,且
是两个不相等的正数,且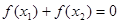 ,求证:
,求证: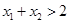 .
. .
. 的单调增区间;
的单调增区间; 在
在 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数m的取值范围.
成立,求实数m的取值范围.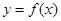 的定义域为R,当
的定义域为R,当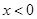 时,
时,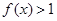 ,且对任意的实数
,且对任意的实数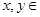 R,等式
R,等式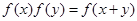 成立.若数列
成立.若数列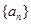 满足
满足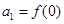 ,且
,且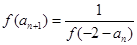 (
(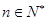 ),则
),则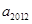 的值为( )
的值为( )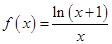 。
。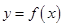 在
在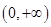 上的单调性;
上的单调性;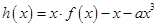 在
在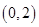 上有极值,求
上有极值,求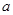 的取值范围。
的取值范围。 在
在 处有极大值,则常数
处有极大值,则常数
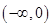 上单调递增的函数是( )
上单调递增的函数是( )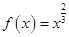
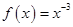
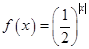
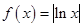
 ,
, 的值域.
的值域.