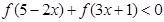题目内容
下列函数为偶函数,且在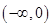 上单调递增的函数是( )
上单调递增的函数是( )
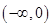 上单调递增的函数是( )
上单调递增的函数是( )A.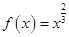 | B.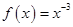 | C.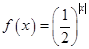 | D.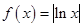 |
C
试题分析:A.
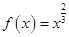 是偶函数,但在
是偶函数,但在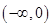 上单调递减的;
上单调递减的;B.
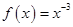 是奇函数;
是奇函数;C. 根据指数函数的图像和函数图像的变换画出函数
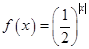 的图像,由图像可知满足题意;
的图像,由图像可知满足题意;D.
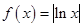 的定义域为
的定义域为 ,所以是非奇非偶函数。
,所以是非奇非偶函数。因此只有C满足题意。
点评:熟练掌握基本初等函数的图像及性质是解决本题的前提条件。判断函数的奇偶性有两步:一求函数的定义域,看定义域是否关于原点对称;二判断
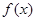 与
与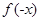 的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。
的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。
练习册系列答案
相关题目

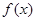 的单调区间;
的单调区间;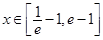 时,
时,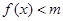 恒成立,求
恒成立,求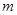 的取值范围;
的取值范围;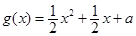 ,若
,若 的图象与
的图象与 上有两个交点,求
上有两个交点,求 的取值范围。
的取值范围。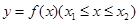 ,设点
,设点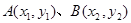 是图象上的两端点.
是图象上的两端点.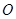 为坐标原点,且点
为坐标原点,且点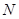 满足
满足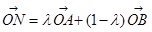 .点
.点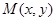 在函数
在函数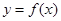 的图象上,且
的图象上,且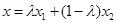 (
(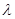 为实数),则称
为实数),则称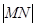 的最大值为函数的“高度”,则函数
的最大值为函数的“高度”,则函数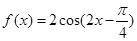 在区间
在区间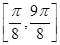 上的“高度”为 .
上的“高度”为 .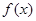 ,在使
,在使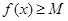 成立的所有常数M中,我们把M的最大值称为函数
成立的所有常数M中,我们把M的最大值称为函数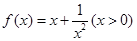 上的“下确界”为 .
上的“下确界”为 .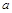 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的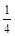 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的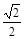 .
.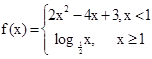 ,若
,若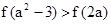 成立,则
成立,则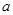 的取值范围是
的取值范围是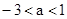
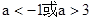

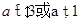
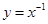 ,
,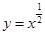 ,
,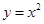 ,
,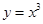 ,,
,,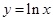 ,
,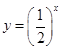 中,在区间
中,在区间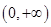 上为减函数的是_________.
上为减函数的是_________.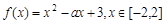 。
。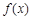 在
在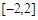 上的最小值是
上的最小值是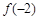 ,试解不等式
,试解不等式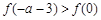 ;
;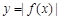 在
在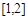 上单调递增,试求实数
上单调递增,试求实数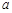 的取值范围。
的取值范围。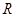 的函数
的函数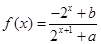 是奇函数。
是奇函数。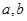 的值;
的值;