题目内容
如图,已知椭圆 的离心率为
的离心率为 ,以椭圆
,以椭圆 的
的
左顶点 为圆心作圆
为圆心作圆 ,设圆
,设圆 与椭圆
与椭圆 交于点
交于点 与点
与点 .
.
(1)求椭圆 的方程;
的方程;
(2)求 的最小值,并求此时圆
的最小值,并求此时圆 的方程;
的方程;
(3)设点 是椭圆
是椭圆 上异于
上异于 、
、 的任意一点,且直线
的任意一点,且直线 、
、 分别与
分别与 轴交于点
轴交于点 、
、 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.
(1)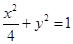 ;(2)
;(2) 的最小值为
的最小值为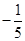 ,此时圆
,此时圆 的方程为
的方程为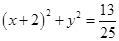 ;
;
(3)详见解析.
解析试题分析:(1)利用圆的方程的求出 的值,然后根据离心率求出
的值,然后根据离心率求出 的值,最后根据
的值,最后根据 、
、 、
、 的关系求出
的关系求出 ,最后确定椭圆的方程;(2)先根据点
,最后确定椭圆的方程;(2)先根据点 、
、 的对称性,设点
的对称性,设点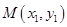 ,将
,将 表示为
表示为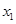 的二次函数,结合
的二次函数,结合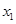 的取值范围,利用二次函数求出
的取值范围,利用二次函数求出 的最小值,从而确定点
的最小值,从而确定点 的坐标,从而确定圆的方程;(3)设点
的坐标,从而确定圆的方程;(3)设点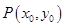 ,求出
,求出 、
、 的方程,从而求出点
的方程,从而求出点 、
、 的坐标,最后利用点
的坐标,最后利用点 在椭圆上来证明
在椭圆上来证明 为定值.
为定值.
(1)依题意,得 ,
,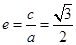 ,
,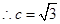 ,
,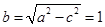 ,
,
故椭圆 的方程为
的方程为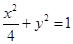 ;
;
(2)点 与点
与点 关于
关于 轴对称,设
轴对称,设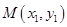 、
、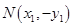 , 不妨设
, 不妨设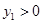 ,
,
由于点 在椭圆
在椭圆 上,所以
上,所以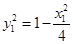 , (*)
, (*)
由已知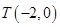 ,则
,则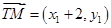 ,
,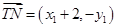 ,
,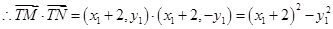 ,
,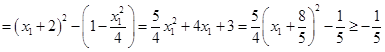 ,
,
由于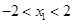 ,故当
,故当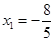 时,
时, 取得最小值为
取得最小值为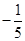 ,
,
由(*)式,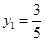 ,故
,故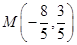 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 ,
,
故圆 的方程为:
的方程为: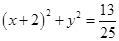 ;
;
(3)设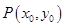 ,则直线
,则直线 的方程为:
的方程为: ,
,
令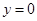 ,得
,得 , 同理:
, 同理: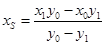 ,
,
故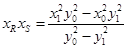 (**)
(**)
又点 与点
与点 在椭圆上,故
在椭圆上,故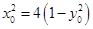 ,
,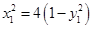 ,
,
代入(**)式,得: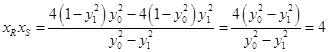
所以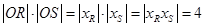 为定值.
为定值.
考点:1.椭圆的方程;2.平面向量的数量积;3.直线与椭圆的位置关系

练习册系列答案
相关题目
 为坐标原点,
为坐标原点, =(
=( ),
), =(1,
=(1, ),
),  .
. 的定义域为[-
的定义域为[- ,
, ],求y=
],求y= 的定义域为[
的定义域为[ 的值.
的值. ,
, , 且
, 且
 的解析式;
的解析式; 时,
时,  的值.
的值. :
: 的焦点为
的焦点为 ,若过点
,若过点 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 .
. 为抛物线
为抛物线 ,
, 为
为 的最小值.
的最小值. ,向量
,向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 求向量
求向量 ,向量
,向量 ,其中
,其中 ,若
,若 试求
试求 的取值范围.
的取值范围. ,b=(
,b=(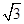 sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b. 上的最大值和最小值.
上的最大值和最小值. ,它们的夹角为
,它们的夹角为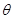 ,且
,且 ,
, ,
, 为正实数.
为正实数. 与
与 垂直,求
垂直,求 ;
; ,求
,求 的最小值及对应的
的最小值及对应的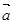 与
与 是否垂直?
是否垂直? 是圆
是圆 (
( , 则
, 则 =
=