题目内容
已知
，
（1）求函数f（x）的定义域；
（2）判断f（x）的奇偶性；并说明理由；
（3）证明f（x）＞0。
，（1）求函数f（x）的定义域；
（2）判断f（x）的奇偶性；并说明理由；
（3）证明f（x）＞0。
解：(1)由
，得x≠0，
所以函数f（x）的定义域为
；
(2)由(1)可知函数f（x）的定义域为
，
，
所以函数f（x）为偶函数。
(3)当x＞0时，
，
所以f（x）＞0；
又因为函数f（x）为偶函数，图象关于y轴对称，
所以当x＜0时，f（x）＞0；
综上可知f（x）＞0。
，得x≠0，所以函数f（x）的定义域为
；(2)由(1)可知函数f（x）的定义域为
，，所以函数f（x）为偶函数。
(3)当x＞0时，
，所以f（x）＞0；
又因为函数f（x）为偶函数，图象关于y轴对称，
所以当x＜0时，f（x）＞0；
综上可知f（x）＞0。
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
．
．
．
，
，
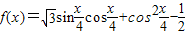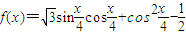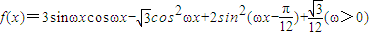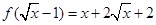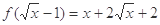