题目内容
1.三棱锥P-ABC的四个顶点都在半径为5的球面上,底面ABC所在的小圆面积为9π,则该三棱锥的高的最大值为( )| A. | 7 | B. | 8 | C. | 8.5 | D. | 9 |
分析 由题意知小圆的半径为3,从而求得球心到小圆的距离为d=$\sqrt{{5}^{2}-{3}^{2}}$=4,从而求高的最大值.
解答 解:由题意知,小圆的半径为3,
故球心到小圆的距离为d=$\sqrt{{5}^{2}-{3}^{2}}$=4,
故则该三棱锥的高的最大值为4+5=9,
故选:D.
点评 本题考查了学生的空间想象力与数形结合的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设i是虚数单位,复数z满足z(1+i)=2i,则复数z的虚部为( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
11.已知三棱锥三视图如图所示,其中俯视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )
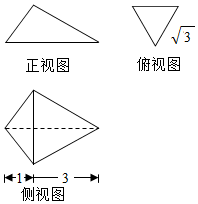

| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 4$\sqrt{3}$ | D. | 16π |
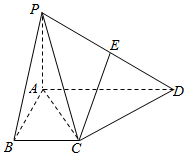 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.