题目内容
20.四边形ABCD为矩形,AB=2,BC=1,O为AB的中点,在矩形ABCD内随机取一点,取到的点到O的距离大于或等于1的概率为( )| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | 1-$\frac{π}{8}$ |
分析 作出图形,在矩形ABCD内随机取一点,取到的点到O的距离大于或等于1包含的区域如图中阴影面积所示,由此利用几何概型能求出取到的点到O的距离大于或等于1的概率.
解答 解: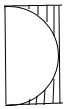 ∵四边形ABCD为矩形,AB=2,BC=1,O为AB的中点,
∵四边形ABCD为矩形,AB=2,BC=1,O为AB的中点,
∴作出图形如右图所示,
在矩形ABCD内随机取一点,
取到的点到O的距离大于或等于1包含的区域如图中阴影面积所示,
∴在矩形ABCD内随机取一点,
取到的点到O的距离大于或等于1的概率为:
p=$\frac{2×1-\frac{1}{2}×π×{1}^{2}}{2×1}$=1-$\frac{π}{4}$.
故选:B.
点评 本题考查概率的求法,考查几何概型等基础知识,考查数据处理能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
11.若向量$\overrightarrow{a}$=(1,0,z)与向量$\overrightarrow{b}$=(2,1,2)的夹角的余弦值为$\frac{2}{3}$,则z等于( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
8.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,(a>0,b>0)的左,右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=5|PF2|,则此双曲线的离心率e的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{3}$ |
 甲、乙两班各随机抽取了5名学生校本课程的学分,用茎叶图表示(如图).s1,s2分别表示甲、乙两班抽取的5名学生学分的标准差,则s1 ( )s2.
甲、乙两班各随机抽取了5名学生校本课程的学分,用茎叶图表示(如图).s1,s2分别表示甲、乙两班抽取的5名学生学分的标准差,则s1 ( )s2.