题目内容
设数列{an}满足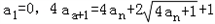 ,令
,令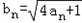 .
.
(1)试判断数列{bn}是否为等差数列?
(2)若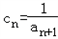 ,求{cn}前n项的和Sn;
,求{cn}前n项的和Sn;
(3)是否存在m,n(m,n∈N*,m≠n)使得1,am,an三个数依次成等比数列?若存在,求出m,n;若不存在,说明理由.
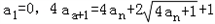 ,令
,令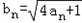 .
.(1)试判断数列{bn}是否为等差数列?
(2)若
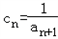 ,求{cn}前n项的和Sn;
,求{cn}前n项的和Sn;(3)是否存在m,n(m,n∈N*,m≠n)使得1,am,an三个数依次成等比数列?若存在,求出m,n;若不存在,说明理由.
解:(1)由已知得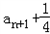 =
=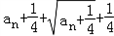 ,
,
∴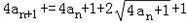 ,
,
∵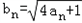
所以bn+12=bn2+2bn+1
∴bn+1=bn+1,
所以数列{bn}为等差数列;
(2)由(1)得:b n+1=bn+1且b1=1,
∴bn=n,即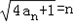 ,
,
∴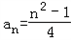 ,
,
∴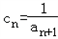 =
=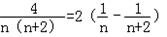 ,则
,则
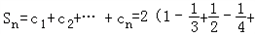
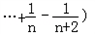
=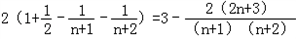 ;
;
(3)设存在m,n满足条件,则有1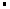 an=am2
an=am2
∴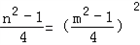 ,
,
即4(n2﹣1)=(m2﹣1)2,所以m2﹣1必为偶数,设为2t,则
n2﹣1=t2,∴n2﹣t2=1
∴(n﹣t)(n+t)=1,
∴有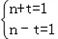 或
或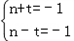 ,
,
即n=1,t=0,
∴m2﹣1=2t=0,
∴m=1与已知矛盾.
∴不存在m,n(m,n∈N*,m≠n)使得1,am,an三个数依次成等比数列.
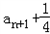 =
=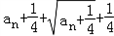 ,
,∴
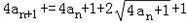 ,
,∵
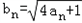
所以bn+12=bn2+2bn+1
∴bn+1=bn+1,
所以数列{bn}为等差数列;
(2)由(1)得:b n+1=bn+1且b1=1,
∴bn=n,即
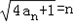 ,
,∴
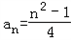 ,
,∴
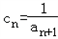 =
=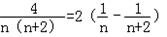 ,则
,则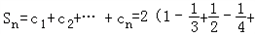
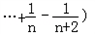
=
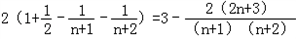 ;
;(3)设存在m,n满足条件,则有1
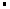 an=am2
an=am2∴
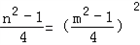 ,
,即4(n2﹣1)=(m2﹣1)2,所以m2﹣1必为偶数,设为2t,则
n2﹣1=t2,∴n2﹣t2=1
∴(n﹣t)(n+t)=1,
∴有
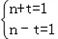 或
或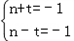 ,
,即n=1,t=0,
∴m2﹣1=2t=0,
∴m=1与已知矛盾.
∴不存在m,n(m,n∈N*,m≠n)使得1,am,an三个数依次成等比数列.

练习册系列答案
相关题目