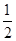题目内容
求函数 的极值
的极值
 的极值
的极值,当 时,
时, 有极大值且极大值为
有极大值且极大值为 ;
;
当 时,
时, 有极小值且极小值为
有极小值且极小值为
 时,
时, 有极大值且极大值为
有极大值且极大值为 ;
;当
 时,
时, 有极小值且极小值为
有极小值且极小值为
试题分析:
求函数的极值,首先找到定义域使得函数有意义,其次求导函数,令其等于零,分析函数的单调性,从而找到极值点,求出极值.
试题解析:
根据题意可知函数定义域为
 ,
,因为
 ,所以
,所以 ,令
,令 ,可得
,可得 ,
,当
 变化时,有下表
变化时,有下表  |  |  |  |  |  |
 |  |  | - |  |  |
 | ↗ |  | ↘ |  | ↗ |
由上表可知,当
 时,
时, 有极大值且极大值为
有极大值且极大值为 ;
;当
 时,
时, 有极小值且极小值为
有极小值且极小值为

练习册系列答案
相关题目

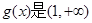 上的增函数,求k的取值范围;
上的增函数,求k的取值范围; 求满足条件的最大整数k的值。
求满足条件的最大整数k的值。 。
。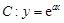 .
.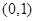 处的切线为
处的切线为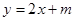 ,求实数
,求实数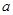 和
和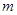 的值;
的值;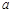 ,曲线
,曲线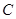 总在直线
总在直线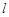 :
: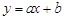 的上方,求实数
的上方,求实数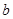 的取值范围.
的取值范围.
 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,求
,求 在区间
在区间 上的最大值;
上的最大值; 时,若
时,若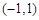 上不单调,求
上不单调,求 的取值范围.
的取值范围.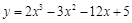 在[0,3]上的最大值和最小值分别是
在[0,3]上的最大值和最小值分别是 ,存在
,存在 ,
, ,则
,则 的最大值为 。
的最大值为 。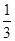 x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )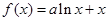 在x=1处取到极值,则a的值为( )
在x=1处取到极值,则a的值为( )