题目内容
已知函数
（1）若
的图象在点
处的切线方程为
，求
在区间
上的最大值；
（2）当
时，若在区间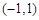
上不单调，求
的取值范围．
（1）若
的图象在点处的切线方程为，求在区间上的最大值；（2）当
时，若在区间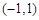上不单调，求的取值范围．解：（1）∵
在上．∴
∵
在上，∴
又
，∴
∴
，解得
∴
由
可知
和
是的极值点．∵
∴
在区间上的最大值为8． （2）因为函数
在区间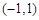不单调，所以函数
在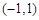上存在零点．而
的两根为
，
，区间长为
，∴在区间
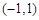上不可能有2个零点．所以
，即
．∵
，∴
．又∵
，∴
．略
练习册系列答案
快乐5加2金卷系列答案
相关题目
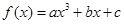在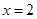
处取得极值为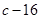
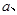
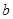的值；（2）若
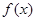有极大值28，求
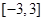上的最小值．
的极值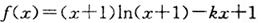
,,k为常数，e是自然对数的底数).
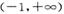上的图象均在第一、二象限？若存在,求出k的最大值；若不存在,请说明理由；
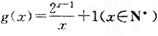，记
，求证：
.
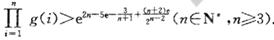
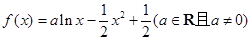的单调区间；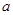
，使得对任意的
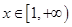，都有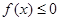
？若存在，求
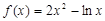的单调递增区间是 。
，
. 
时，求函数
的极值；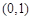 
上是单调增函数，求实数
的取值范围.
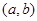，其中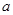
表示第一次抛掷的结果，
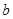表示第二次抛掷的结果，则函数
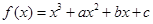有极值点的概率为（ ）
的单调递增区间是