题目内容
下列函数中,最小值不是2的是( )
A、f(x)=x+
| ||
| B、f(x)=3+sinx | ||
| C、f(x)=3x+3-x | ||
| D、f(x)=log2x+logx2 |
考点:基本不等式,函数的最值及其几何意义
专题:函数的性质及应用
分析:由基本不等式和函数的图象或性质逐个选项判断即可.
解答:
解:选项A,由x>0和基本不等式可得f(x)=x+
≥2
=2,
当且仅当x=
即x=1时取等号,即最小值为2,正确;
选项B,sinx的最小值为-1,故f(x)=3+sinx的最小值为2,正确;
选项C,f(x)=3x+3-x=3x+
≥2
=2,
当且仅当3x=
即x=0时取等号,即最小值为2,正确;
选项D,若log2x为负值,显然不满足最小值为2,故错误.
故选:D
| 1 |
| x |
x•
|
当且仅当x=
| 1 |
| x |
选项B,sinx的最小值为-1,故f(x)=3+sinx的最小值为2,正确;
选项C,f(x)=3x+3-x=3x+
| 1 |
| 3x |
3x•
|
当且仅当3x=
| 1 |
| 3x |
选项D,若log2x为负值,显然不满足最小值为2,故错误.
故选:D
点评:本题考查函数式的最值,涉及基本不等式和函数的最值,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,不等式
(a为常数)表示的平面区域的面积为8,则
的最小值为( )
|
| x+y+2 |
| x+3 |
A、8
| ||
B、5-4
| ||
C、6-4
| ||
D、
|
在(x+y)n的展开式中,若第8项系数最大,则n的值可能等于( )
| A、14,15 |
| B、15,16 |
| C、16,17 |
| D、13,14,15 |
如图所示的是一个算法的流程图,当输入x的值为2014时,输出y的值为 ( )


| A、1 | ||
B、
| ||
C、
| ||
| D、9 |
在△ABC中,
•
=
•
,则△ABC是( )
| CB |
| CA |
| BC |
| BA |
| A、等腰直角三角形 |
| B、等边三角形 |
| C、等腰三角形 |
| D、直角三角形 |
阅读如图的程序框图,运行相应的程序,若输出S=
,则判断框内应填入( )

| 2013 |
| 2014 |

| A、i≥2014 |
| B、i≥2015 |
| C、i>2014 |
| D、i>2015 |
执行如图所示的程序框图,输出的结果是15,则a的初始值m(m>0)有多少种可能( )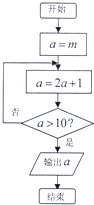

| A、1 | B、2 | C、3 | D、4 |