题目内容
(本小题满分13分)
已知椭圆C: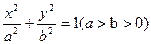 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为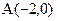 ,
,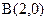 ,离心率
,离心率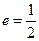 。
。
(Ⅰ)求椭圆C的方程:
(Ⅱ)设椭圆的两焦点分别为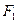 ,
,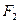 ,点P是其上的动点,
,点P是其上的动点,
(1)当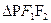 内切圆的面积最大时,求内切圆圆心的坐标;
内切圆的面积最大时,求内切圆圆心的坐标;
(2)若直线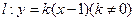 与椭圆交于
与椭圆交于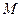 、
、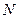 两点,证明直线
两点,证明直线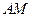 与直线
与直线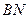 的交点在直线
的交点在直线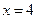 上。
上。
已知椭圆C:
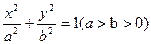 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为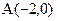 ,
,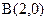 ,离心率
,离心率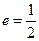 。
。(Ⅰ)求椭圆C的方程:
(Ⅱ)设椭圆的两焦点分别为
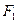 ,
,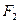 ,点P是其上的动点,
,点P是其上的动点,(1)当
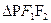 内切圆的面积最大时,求内切圆圆心的坐标;
内切圆的面积最大时,求内切圆圆心的坐标;(2)若直线
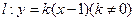 与椭圆交于
与椭圆交于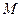 、
、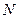 两点,证明直线
两点,证明直线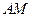 与直线
与直线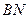 的交点在直线
的交点在直线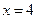 上。
上。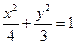
(1)
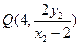
(2).直线
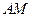 与直线
与直线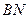 的交点住直线
的交点住直线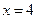 上.
上.解:(Ⅰ)椭圆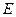 的方程
的方程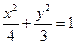 ……3分
……3分
(Ⅱ)(1)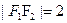 ,设
,设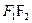 边上的高为
边上的高为 ,
,
设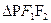 的内切圆的半径为
的内切圆的半径为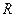 ,因为
,因为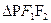 的周长为定值6.
的周长为定值6.
所以 ……5分
……5分
 当P在椭圆上顶点时,
当P在椭圆上顶点时, 最大为
最大为 ,
,
故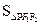 的最大值为
的最大值为 ,
,
于是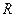 也随之最大值为
也随之最大值为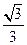
此时内切圆圆心的坐标为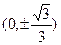 ……7分
……7分
(2)将直线 代入椭圆
代入椭圆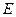 的方程
的方程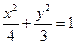 并整理.
并整理.
得 .
.
设直线 与椭圆
与椭圆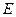 的C交点
的C交点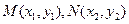 ,
,
由根系数的关系,得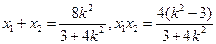 . ……9分
. ……9分
直线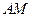 的方程为:
的方程为: ,它与直线
,它与直线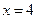 的交点坐标为
的交点坐标为
 同理可求得直线
同理可求得直线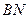 与直线
与直线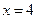 的交点坐标为
的交点坐标为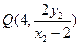 .…11分
.…11分
下面证明 、
、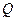 两点重合,即证明
两点重合,即证明 、
、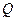 两点的纵坐标相等:
两点的纵坐标相等:
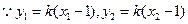 ,
,
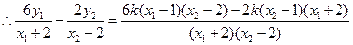
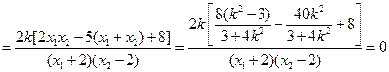
因此结论成立.
综上可知.直线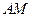 与直线
与直线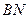 的交点住直线
的交点住直线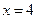 上. ……………13分
上. ……………13分
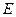 的方程
的方程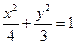 ……3分
……3分(Ⅱ)(1)
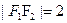 ,设
,设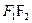 边上的高为
边上的高为 ,
,
设
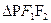 的内切圆的半径为
的内切圆的半径为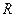 ,因为
,因为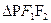 的周长为定值6.
的周长为定值6.所以
 ……5分
……5分 当P在椭圆上顶点时,
当P在椭圆上顶点时, 最大为
最大为 ,
,故
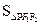 的最大值为
的最大值为 ,
,于是
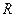 也随之最大值为
也随之最大值为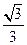
此时内切圆圆心的坐标为
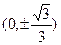 ……7分
……7分(2)将直线
 代入椭圆
代入椭圆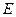 的方程
的方程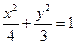 并整理.
并整理.得
 .
.设直线
 与椭圆
与椭圆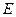 的C交点
的C交点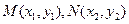 ,
,由根系数的关系,得
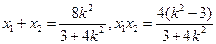 . ……9分
. ……9分直线
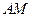 的方程为:
的方程为: ,它与直线
,它与直线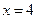 的交点坐标为
的交点坐标为 同理可求得直线
同理可求得直线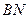 与直线
与直线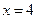 的交点坐标为
的交点坐标为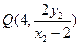 .…11分
.…11分下面证明
 、
、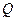 两点重合,即证明
两点重合,即证明 、
、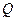 两点的纵坐标相等:
两点的纵坐标相等: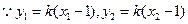 ,
,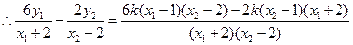
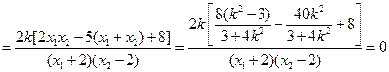
因此结论成立.
综上可知.直线
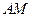 与直线
与直线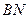 的交点住直线
的交点住直线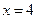 上. ……………13分
上. ……………13分
练习册系列答案
相关题目
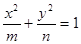 表示焦点在x轴上的椭圆有
表示焦点在x轴上的椭圆有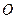 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为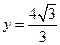 ,离心率
,离心率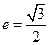 ,
,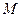 是椭圆上的动点.
是椭圆上的动点.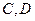 的坐标分别是
的坐标分别是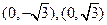 ,求
,求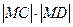 的最大值;
的最大值;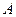 的坐标为
的坐标为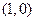 ,
,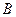 是圆
是圆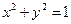 上的点,点
上的点,点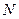 是点
是点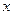 轴上的射影,点
轴上的射影,点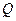 满足条件:
满足条件: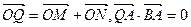 ,求线段
,求线段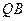 的中点
的中点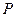 的轨迹方程.
的轨迹方程.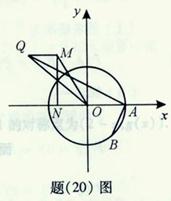
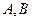 是圆
是圆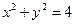 上满足条件
上满足条件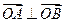 的两个点,其中
的两个点,其中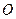 是坐标原点,分别过
是坐标原点,分别过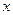 轴的垂线段,交椭圆
轴的垂线段,交椭圆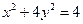 于
于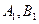 点,动点
点,动点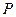 满足
满足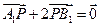
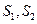 分别表示
分别表示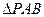 和
和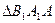 的面积,当点
的面积,当点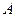 在
在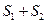 的最大面积.(12分)
的最大面积.(12分)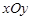 中,已知△
中,已知△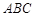 顶点
顶点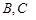
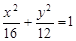 的两个焦点,顶点
的两个焦点,顶点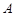 在该椭圆上,则
在该椭圆上,则 =_______________.
=_______________.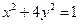 的离心率为( )
的离心率为( )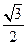


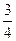
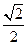
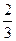
 的中心为原点,离心率
的中心为原点,离心率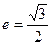 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线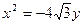 的焦点重合,则此椭圆方程为 ( )
的焦点重合,则此椭圆方程为 ( )



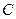 :
: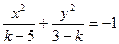 ,则“
,则“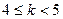 ”是“曲线C表示焦点在
”是“曲线C表示焦点在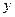 轴上的椭圆”的______________条件.
轴上的椭圆”的______________条件.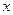 轴上的椭圆
轴上的椭圆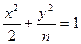 的离心率为
的离心率为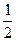 ,则
,则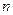 =( )
=( )