题目内容
已知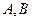 是圆
是圆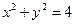 上满足条件
上满足条件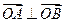 的两个点,其中
的两个点,其中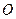 是坐标原点,分别过
是坐标原点,分别过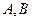 作
作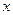 轴的垂线段,交椭圆
轴的垂线段,交椭圆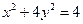 于
于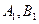 点,动点
点,动点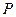 满足
满足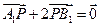
(I)求动点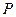 的轨迹方程.
的轨迹方程.
(II)设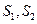 分别表示
分别表示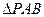 和
和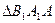 的面积,当点
的面积,当点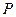 在
在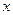 轴的上方,点
轴的上方,点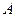 在
在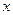 轴的下方时,求
轴的下方时,求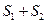 的最大面积.(12分)
的最大面积.(12分)
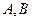 是圆
是圆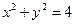 上满足条件
上满足条件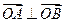 的两个点,其中
的两个点,其中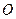 是坐标原点,分别过
是坐标原点,分别过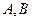 作
作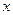 轴的垂线段,交椭圆
轴的垂线段,交椭圆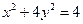 于
于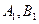 点,动点
点,动点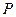 满足
满足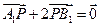
(I)求动点
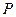 的轨迹方程.
的轨迹方程.(II)设
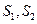 分别表示
分别表示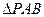 和
和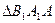 的面积,当点
的面积,当点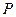 在
在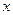 轴的上方,点
轴的上方,点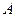 在
在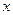 轴的下方时,求
轴的下方时,求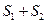 的最大面积.(12分)
的最大面积.(12分)(I)
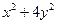
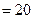
(II)2
解:(I)设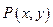 ,
, 则
则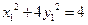 ①;
①;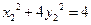 ②
②
从而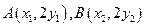
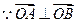
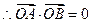 即
即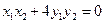 ③
③
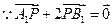
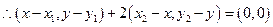
即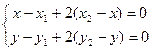
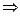
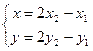
于是得
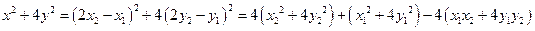
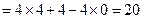
所以动点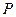 的轨迹方程为
的轨迹方程为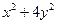
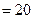 (6分)
(6分)
(II)根据(I)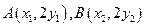 ,所以直线
,所以直线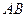 的方程为
的方程为
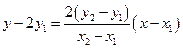
即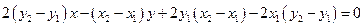
从而点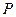
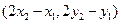
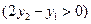 到直线
到直线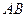 的距离为
的距离为
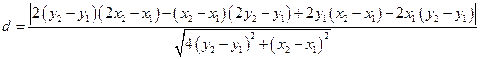
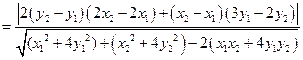
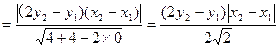
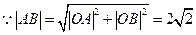
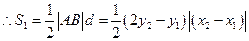
而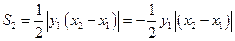
所以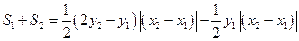
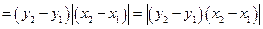
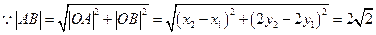
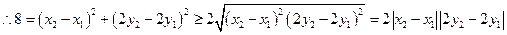
当且仅当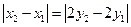 时取等号
时取等号
所以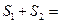
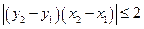
即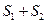 的最大值为
的最大值为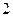 (12分)
(12分)
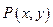 ,
, 则
则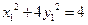 ①;
①;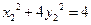 ②
②从而
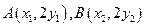
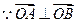
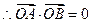 即
即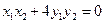 ③
③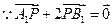
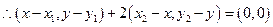
即
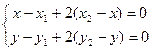
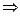
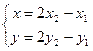
于是得
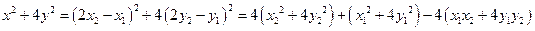
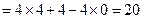
所以动点
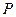 的轨迹方程为
的轨迹方程为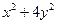
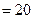 (6分)
(6分)(II)根据(I)
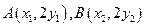 ,所以直线
,所以直线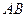 的方程为
的方程为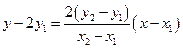
即
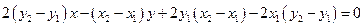
从而点
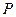
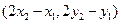
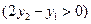 到直线
到直线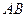 的距离为
的距离为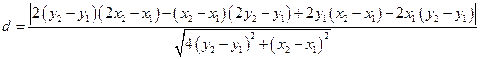
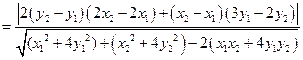
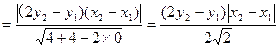
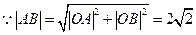
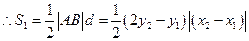
而
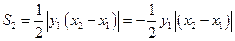
所以
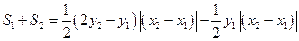
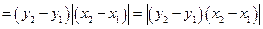
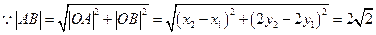
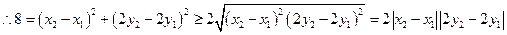
当且仅当
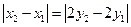 时取等号
时取等号所以
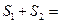
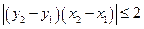
即
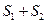 的最大值为
的最大值为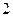 (12分)
(12分)
练习册系列答案
相关题目
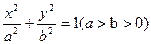 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为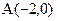 ,
,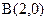 ,离心率
,离心率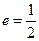 。
。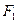 ,
,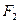 ,点P是其上的动点,
,点P是其上的动点,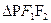 内切圆的面积最大时,求内切圆圆心的坐标;
内切圆的面积最大时,求内切圆圆心的坐标;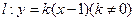 与椭圆交于
与椭圆交于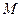 、
、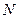 两点,证明直线
两点,证明直线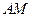 与直线
与直线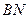 的交点在直线
的交点在直线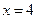 上。
上。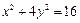 有相同焦点,且椭圆C上一点P到两焦点的距离之和等于
有相同焦点,且椭圆C上一点P到两焦点的距离之和等于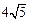 ,求椭圆C的标准方程;
,求椭圆C的标准方程;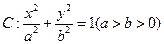 的上项点为B1,右、右焦点为F1、F2,
的上项点为B1,右、右焦点为F1、F2,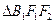 是面积为
是面积为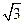 的等边三角形。
的等边三角形。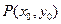 是以线段F1F2为直径的圆上一点,且
是以线段F1F2为直径的圆上一点,且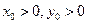 ,求过P点与该圆相切的直线
,求过P点与该圆相切的直线 的方程;
的方程;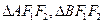 的重心分别为G、H,请问原点O在以线段GH为直径的圆内吗?若在请说明理由。
的重心分别为G、H,请问原点O在以线段GH为直径的圆内吗?若在请说明理由。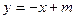 与曲线
与曲线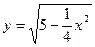 只有一个公共点,则m的取值范围是( )
只有一个公共点,则m的取值范围是( )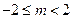
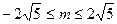
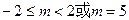
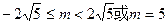
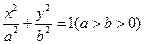 的离心率为
的离心率为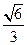 ,过
,过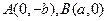 的直线与原点的距离为
的直线与原点的距离为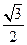
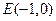 ,直线
,直线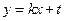 与椭圆交于不同两点C,D,试问:对任意的
与椭圆交于不同两点C,D,试问:对任意的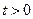 ,是否都存在实数
,是否都存在实数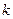 ,使得以线段CD为直径的圆过点E?证明你的结论
,使得以线段CD为直径的圆过点E?证明你的结论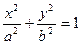
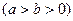 的离心率为
的离心率为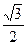 ,则双曲
,则双曲 的离心率为( )
的离心率为( )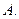

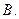
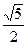
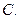
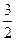
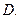
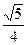
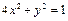 及直线
及直线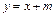 ,当直线被椭圆截得的弦最长时的直线方程为
,当直线被椭圆截得的弦最长时的直线方程为