题目内容
2.求下列函数的零点个数:(1)f(x)=log${\;}_{\frac{2}{3}}$x+x2-2;
(2)f(x)=3x-log${\;}_{\frac{1}{2}}$x.
分析 令f(x)=0,得出两个函数相等,作出两个函数图象,观察函数图象的交点个数来判断零点个数.
解答 解:(1)令f(x)=0得log${\;}_{\frac{2}{3}}$x=2-x2.
分别作出y=log${\;}_{\frac{2}{3}}$x和y=2-x2的函数图象,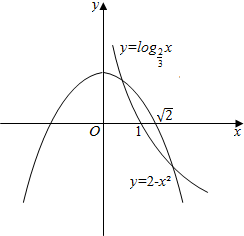
由图象可知y=log${\;}_{\frac{2}{3}}$x和y=2-x2有两个交点,
∴f(x)=log${\;}_{\frac{2}{3}}$x+x2-2有两个零点.
(2)令f(x)=0得3x=log${\;}_{\frac{1}{2}}$x.
分别作出y=3x和y=log${\;}_{\frac{1}{2}}$x的函数图象,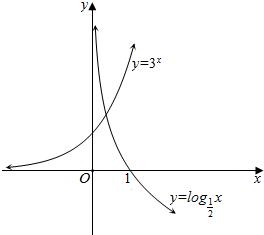
由图象可知y=3x和y=log${\;}_{\frac{1}{2}}$x有1个交点,
∴f(x)=3x-log${\;}_{\frac{1}{2}}$x有1个零点.
点评 本题考查了函数零点个数的判断,作出函数图象是解题关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
12.已知α>0且a≠1,函数f(x)=$\left\{\begin{array}{l}{(a-1)x+3a-4,(x≤0)}\\{{a}^{x},(x>0)}\end{array}\right.$满足对任意实数x1≠x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)成立,则a的取值范围是( )
| A. | $(1,\frac{5}{3}]$ | B. | (0,1) | C. | (1,+∞) | D. | $[\frac{5}{3},2)$ |
13.集合A={x|y=log2(x+1)},B={-1,0,1},则A∩B等于( )
| A. | {0,1} | B. | {-1,0,1} | C. | {0} | D. | {1} |
12.函数f(x)=sin2(2x+$\frac{π}{3}$)的导数是( )
| A. | f′(x)=2sin(2x+$\frac{π}{3}$) | B. | f′(x)=4sin(2x+$\frac{π}{3}$) | C. | f′(x)=sin(4x+$\frac{2π}{3}$) | D. | f′(x)=2sin(4x+$\frac{2π}{3}$) |
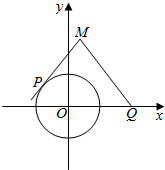 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.