题目内容
如图,直角坐标系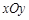 中,一直角三角形
中,一直角三角形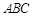 ,
,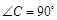 ,B、D在
,B、D在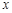 轴上且关于原点
轴上且关于原点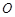 对称,
对称,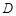 在边
在边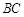 上,BD=3DC,△ABC的周长为12.若一双曲线
上,BD=3DC,△ABC的周长为12.若一双曲线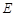 以B、C为焦点,且经过A、D两点.
以B、C为焦点,且经过A、D两点.
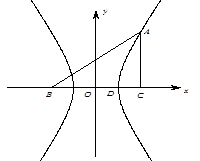
⑴ 求双曲线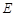 的方程;
的方程;
⑵ 若一过点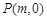 (
(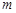 为非零常数)的直线
为非零常数)的直线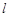 与双曲线
与双曲线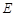 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点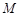 、
、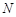 ,且
,且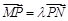 ,问在
,问在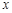 轴上是否存在定点
轴上是否存在定点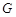 ,使
,使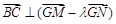 ?若存在,求出所有这样定点
?若存在,求出所有这样定点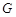 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
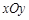 中,一直角三角形
中,一直角三角形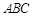 ,
,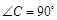 ,B、D在
,B、D在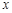 轴上且关于原点
轴上且关于原点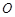 对称,
对称,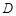 在边
在边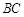 上,BD=3DC,△ABC的周长为12.若一双曲线
上,BD=3DC,△ABC的周长为12.若一双曲线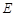 以B、C为焦点,且经过A、D两点.
以B、C为焦点,且经过A、D两点.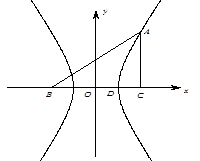
⑴ 求双曲线
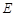 的方程;
的方程;⑵ 若一过点
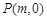 (
(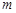 为非零常数)的直线
为非零常数)的直线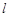 与双曲线
与双曲线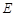 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点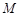 、
、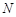 ,且
,且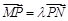 ,问在
,问在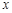 轴上是否存在定点
轴上是否存在定点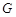 ,使
,使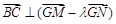 ?若存在,求出所有这样定点
?若存在,求出所有这样定点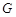 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由(1) 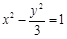 (2)在
(2)在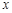 轴上存在定点
轴上存在定点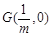 ,使
,使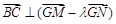 .
.
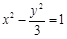 (2)在
(2)在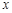 轴上存在定点
轴上存在定点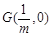 ,使
,使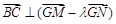 .
. 试题分析:(1) 设双曲线
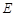 的方程为
的方程为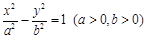 ,则
,则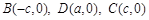 .
.由
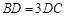 ,得
,得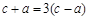 ,即
,即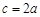 .
.∴
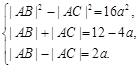 3分
3分解之得
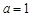 ,∴
,∴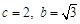 .
.∴双曲线
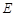 的方程为
的方程为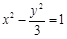 . 5分
. 5分(2) 设在
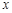 轴上存在定点
轴上存在定点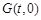 ,使
,使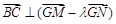 .
.设直线
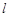 的方程为
的方程为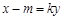 ,
,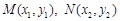 .
.由
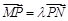 ,得
,得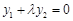 .
.即
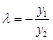 ① 6分
① 6分∵
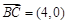 ,
,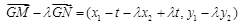 ,
,∴
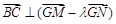
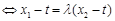 .
.即
 . ② 8分
. ② 8分把①代入②,得
 ③ 9分
③ 9分把
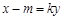 代入
代入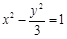 并整理得
并整理得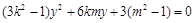
其中
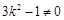 且
且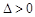 ,即
,即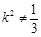 且
且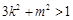 .
.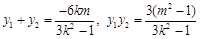 . 10分
. 10分代入③,得
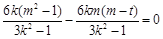 ,化简得
,化简得 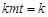 .当
.当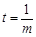 时,上式恒成立.
时,上式恒成立.因此,在
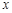 轴上存在定点
轴上存在定点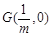 ,使
,使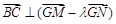 . 13分
. 13分点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(1)求双曲线方程时,应用了双曲线的定义及其几何性质,难度不大,较为典型。(2)则在应用韦达定理的基础上,通过平面向量的坐标运算,达到证明目的。

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
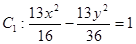 ,点
,点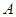 、
、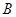 分别为双曲线
分别为双曲线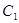 的左、右焦点,动点
的左、右焦点,动点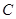 在
在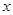 轴上方.
轴上方.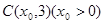 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以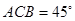 ,求△
,求△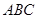 的外接圆的方程;
的外接圆的方程;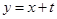 上任取一点
上任取一点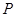 ,从点
,从点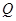 . 问是否存在一个定点
. 问是否存在一个定点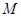 ,恒有
,恒有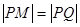 ?请说明理由.
?请说明理由.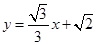 与圆心为D的圆
与圆心为D的圆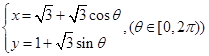 交于A、B两点,则直线AD与BD的倾斜角之和为( )
交于A、B两点,则直线AD与BD的倾斜角之和为( )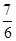 π
π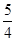 π
π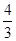 π
π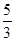 π
π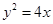 上任意一点
上任意一点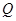 ,点
,点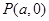 都满足
都满足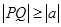 ,则
,则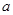 的取值范围是____ .
的取值范围是____ . 的两个端点
的两个端点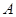 、
、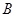 分别分别在
分别分别在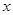 轴、
轴、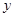 轴上滑动,
轴上滑动,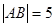 ,点
,点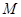 是
是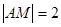 ,点
,点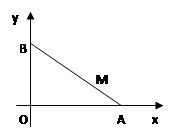
 为点
为点 为右焦点,过
为右焦点,过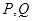 两点,求
两点,求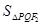 的最大值,并求此时直线
的最大值,并求此时直线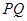 的方程.
的方程.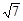 ,0),直线
,0),直线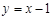 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为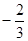 ,则此双曲线的方程是 .
,则此双曲线的方程是 . 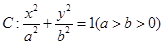 的离心率为
的离心率为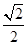 ,
,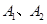 是椭圆的左右顶点,
是椭圆的左右顶点,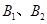 是椭圆的上下顶点,四边形
是椭圆的上下顶点,四边形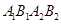 的面积为
的面积为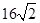 .
.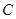 的方程;
的方程;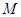 过
过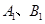 两点.当圆心
两点.当圆心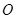 的距离最小时,求圆
的距离最小时,求圆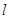 的斜率为2且过抛物线
的斜率为2且过抛物线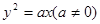 的焦点F,又与
的焦点F,又与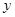 轴交于点A,
轴交于点A,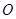 为坐标原点,若
为坐标原点,若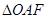 的面积为4,则抛物线的方程为:
的面积为4,则抛物线的方程为: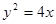
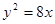
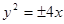
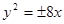
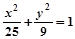 (y≠0)
(y≠0)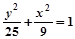 (y≠0)
(y≠0)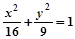 (y≠0)
(y≠0)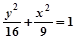 (y≠0)
(y≠0)