题目内容
函数y=exsinx在[0，π]上的单调递增区间是 ．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先对函数f（x）进行求导，求函数f（x）的单调递增区间即求f′（x）≥0的x的区间．
解答：
解：∵f′（x）=ex（sinx+cosx），
若函数y=exsinx在[0，π]上的单调递增，
只需f′（x）=ex•
sin（x+
）≥0即可，
解得：0≤x≤
，
故答案为：[0，
]．
若函数y=exsinx在[0，π]上的单调递增，
只需f′（x）=ex•
| 2 |
| π |
| 4 |
解得：0≤x≤
| 3π |
| 4 |
故答案为：[0，
| 3π |
| 4 |
点评：本题主要考查通过求函数的导数确定函数增减区间的问题．当导数大于0时函数单调递增，当导数小于0时函数单调递减．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是梯形，BC∥AD，∠ABC=90°，AB=BC=PA=1，AD=2，E，F分别为PA，AD的中点．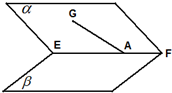
平面角为锐角的二面角α-EF-β，A∈EF，AG?α，∠GAE=45°，若AG与β所成角为30°，则二面角α-EF-β的大小是