题目内容
1．若实数x，y满足$\left\{\begin{array}{l}2x+y≤4\\ x+3y≤7\\ x≥0\\ y≥0\end{array}\right.$则z=3x+2y的最大值为7．分析 作出不等式组对应的平面区域，利用目标函数的几何意义，求最大值．
解答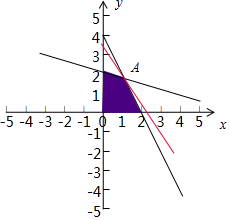 
解：作出不等式组对应的平面区域如图：（阴影部分）．
由z=3x+2y得y=-$\frac{3}{2}$x+$\frac{1}{2}$z
平移直线y=-$\frac{3}{2}$x+$\frac{1}{2}$z，
由图象可知当直线y=-$\frac{3}{2}$x+$\frac{1}{2}$z经过点A时，直线y=-$\frac{3}{2}$x+$\frac{1}{2}$z的截距最大，
此时z最大．
由$\left\{\begin{array}{l}{2x+y=4}\\{x+3y=7}\end{array}\right.$，解得A（1，2），
代入目标函数z=3x+2y得z=3×1+2×2=7．
即目标函数z=3x+2y的最大值为7．
故答案为：7．
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
相关题目
11．点A（sin2017°，cos2017°）在直角坐标平面上位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
9．已知集合P={x|1＜3x≤9}，Q={1，2，3}，则P∩Q=（ ）
| A． | {1} | B． | {1，2} | C． | {2，3} | D． | {1，2，3} |
16．已知函数f（x）=-Acos（ωx+ϕ）+$\sqrt{3}$Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜$\frac{π}{2}$）的最大值为2，周期为π，将函数y=f（x）图象向右平移$\frac{π}{12}$个单位得到函数y=g（x）的图象，若函数y=g（x）是偶函数，则函数f（x）的一条对称轴为（ ）
| A． | x=-$\frac{π}{6}$ | B． | x=$\frac{π}{12}$ | C． | x=-$\frac{π}{12}$ | D． | x=$\frac{π}{3}$ |
13．平面直角坐标系xOy中，角α的始边在x轴非负半轴，终边与单位圆交于点$A（\frac{3}{5}，\frac{4}{5}）$，将其终边绕O点逆时针旋转$\frac{3π}{4}$后与单位圆交于点B，则B的横坐标为（ ）
| A． | $-\frac{{\sqrt{2}}}{10}$ | B． | $-\frac{{7\sqrt{2}}}{10}$ | C． | $-\frac{{3\sqrt{2}}}{4}$ | D． | $-\frac{{4\sqrt{2}}}{5}$ |
如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，BA=2，AC=1，B1C=3