题目内容
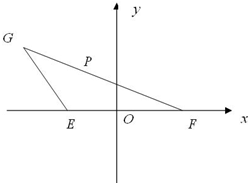 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|. |
| FG |
. |
| EF |
. |
| PE |
| 1 |
| 2 |
. |
| EG |
. |
| EG |
(1)求P的轨迹C的方程;
(2)A、B为轨迹C上任意两点,且
. |
| OE |
. |
| OA |
. |
| OB |
分析:(1)取EG的中点为H,利用
+
=
∴
•
=0推出|PE|+|PF|=|GF|=10>|EF|=6∴P点的轨迹是以E、F为焦点,长轴长为10的椭圆
设其轨迹方程为
+
=1,求出a,c,b解得
+
=1即可.
(2)利用
=α
+(1-α)
=α
+
-α
推出A、B、E三点共线,设AB所在直线方程为x=my-3,结合韦达定理,求出S△DEM=
|
||yM|的表达式
利用基本不等式16|m|+
≥40,求出S△DEM最大值为
.
| PE |
| 1 |
| 2 |
| EG |
| PH |
| PH |
| EG |
设其轨迹方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 16 |
(2)利用
| OE |
| OA |
| OB |
| OA |
| OB |
| OB |
推出A、B、E三点共线,设AB所在直线方程为x=my-3,结合韦达定理,求出S△DEM=
| 1 |
| 2 |
| OE |
| 72 | ||
16|m|+
|
| 25 |
| |m| |
| 9 |
| 5 |
解答:解:(1)取EG的中点为H,则
+
=
∴
•
=0∴PH⊥GE∴PH是EG的垂直平分线(2分)∴|PE|=|PG|∴|PE|+|PF|=|GF|=10>|EF|=6∴P点的轨迹是以E、F为焦点,长轴长为10的椭圆(4分)
设其轨迹方程为
+
=1,则2a=10,a=5,2c=6,c=3,b2=a2-c2=16∴
+
=1(5分)
(2)∵
=α
+(1-α)
=α
+
-α
∴
-
=α(
-
)
∴
=α
∴A、B、E三点共线
∵E(-3,0)设AB所在直线方程为x=my-3
整理关于y的方程为:(16m2+25)y2-96my-256=0(△>0恒成立)
∴y1+y2=
M点的纵坐标为yM=
=
(9分)
∴S△DEM=
|
||yM|=
×3×
=
=
(10分)
∴当16|m|=
,即m=±
时,16|m|+
≥40,S△DEM最大值为
.(12分)
| PE |
| 1 |
| 2 |
| EG |
| PH |
| PH |
| EG |
设其轨迹方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 16 |
(2)∵
| OE |
| OA |
| OB |
| OA |
| OB |
| OB |
∴
| OE |
| OB |
| OA |
| OB |
∴
| BE |
| BA |
∵E(-3,0)设AB所在直线方程为x=my-3
|
整理关于y的方程为:(16m2+25)y2-96my-256=0(△>0恒成立)
∴y1+y2=
| 96m |
| 16m2+25 |
| y1+y2 |
| 2 |
| 48m |
| 16m2+25 |
∴S△DEM=
| 1 |
| 2 |
| OE |
| 1 |
| 2 |
| 48|m| |
| 16m2+25 |
| 72|m| |
| 16m2+25 |
| 72 | ||
16|m|+
|
∴当16|m|=
| 25 |
| |m| |
| 5 |
| 4 |
| 25 |
| |m| |
| 9 |
| 5 |
点评:本题是中档题,考查向量的数量积,三角形的面积公式,韦达定理,基本不等式的应用,考查计算能力,转化思想,常考题型.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
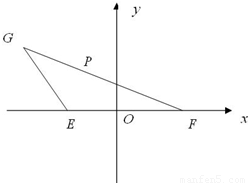 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,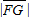 =10,
=10,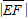 =6,
=6,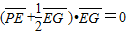
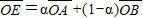 ,M为AB的中点,求△OEM面积的最大值.
,M为AB的中点,求△OEM面积的最大值.