题目内容
已知sinα=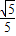 ,sin(α-β)=-
,sin(α-β)=-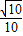 ,α,β均为锐角,则β等于 .
,α,β均为锐角,则β等于 .
【答案】分析:遇到有这样表示的角的三角函数问题,解题时通常用整体思想来处理,β=(β-α)+α,根据条件中所给的角的范围和两个三角函数值,用两角和的正弦公式展开,得到结果.
解答:解:∵sin(α-β)=-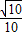 ,
,
∴sin(β-α)=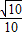 ,
,
∵α,β均为锐角,
∴cos(β-α)=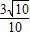 ,
,
cosα=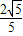 ,
,
∴cosβ=cos[(β-α)+α]=cos(β-α)cosα-sin(β-α)cosα
=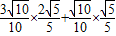 =
=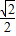 ,
,
∵β均为锐角,
∴β=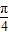 .
.
点评:已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种.
解答:解:∵sin(α-β)=-
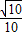 ,
,∴sin(β-α)=
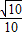 ,
,∵α,β均为锐角,
∴cos(β-α)=
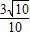 ,
,cosα=
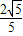 ,
,∴cosβ=cos[(β-α)+α]=cos(β-α)cosα-sin(β-α)cosα
=
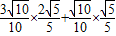 =
=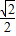 ,
,∵β均为锐角,
∴β=
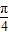 .
.点评:已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
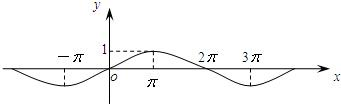 已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象向右平移
已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象向右平移| 2π |
| 3 |
A、sin(2x-
| ||||
B、sin(2x-
| ||||
C、sin(
| ||||
D、sin(
|
已知
=-
,则cosα+sinα等于( )
| cos(π-2α) | ||
sin(α-
|
| ||
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|