题目内容

13．函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列式子正确的是（　　）
A．0＜f′（1）＜f′（2）＜f（2）-f（1）B．0＜f′（2）＜f（2）-f（1）＜f′（1）C．0＜f′（2）＜f′（1）＜f（2）-f（1）D．0＜f（2）-f（1）＜f′（1）＜f′（2）

分析 利用导数的几何意义，直线的斜率，判断求解即可．

解答 解：函数f（x）的图象如图所示，f′（x）是f（x）的导函数，
可知函数在x∈[1，2]是增函数，0＜f′（2）＜f′（1），
$\frac{f（2）-f（1）}{2-1}$∈（f′（2），f′（1）），
故选：B．

点评 本题考查函数的图象的应用，导函数的几何意义，考查计算能力．

练习册系列答案
相关题目
3．已知函数f（x）在其定义区间[a，b]上满足①f（x）＞0；②f′（x）＜0；③对任意的x1，x2∈[a，b]，式子$f（{\frac{{{x_1}+{x_2}}}{2}}）$≤$\frac{{f（{x_1}）+f（{x_2}）}}{2}$恒成立．记S1=$\int_{\;\;a}^{\;\;b}$f（x）dx，S2=$\frac{f（a）+f（b）}{2}$•（b-a），S3=f（b）（b-a），则S1，S2，S3的大小关系为s3＜s1≤s2．（按由小到大的顺序）
4．化简：$\frac{1}{{sin{{10}°}}}$-$\frac{{\sqrt{3}}}{{cos{{10}°}}}$的结果是（　　）
A．1B．$\sqrt{3}$C．2D．4
1．在△ABC中，D为BC的中点，tan∠BAD=$\frac{1}{tan∠C}$，E为边AC上的一点，且AE=$\frac{1}{2}$EC，BE=2，则△ABC面积的最大值为3．
8．如图为某算法的程序框图，该算法的程序运行后输出的结果为299，则实数M的取值范围是（　　）
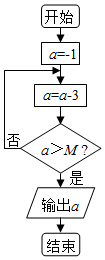
A．296＜M＜299B．296≤M＜299C．296＜M≤299D．296≤M≤299
18．已知集合A={x∈R|0＜log2x＜1}，B={y∈R|y=2-x2}，则A∩B=（　　）
A．∅B．（0，2]C．（1，2）D．（1，2]
5．在平面直角坐标系xOy中，已知A（cosα，sinα），B（cosβ，sinβ）是直线y=$\sqrt{3}$x+$\sqrt{2}$上的两点，则tan（α+β）的值为-$\sqrt{3}$．
2．若安排期中考试的科目有6门，则语文必须在数学之前考的排法有（　　）
A．720种B．360种C．240种D．120种
8．计算不定积分${∫}_{\;}^{\;}$（$\frac{2{x}^{2}+2x-1}{\sqrt{x}}$）dx．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网