题目内容
已知函数
是幂函数且在
上为减函数，函数
在区间
上的最大值为2，试求实数
的值。
，
解析试题分析：解：因为函数是幂函数且在上为减函数，所以有
，解得，
①当
是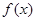
的单调递减区间，
②当
，
解得
③
，解得
综合①②③可知
考点：函数的单调性；函数的最大值
点评：本题需懂得幂函数的形式：
，
为常数。另外，涉及到函数的最值，常要结合到函数的单调性。
练习册系列答案
阅读快车系列答案
相关题目
.
成立的
的取值范围；
，
，求实数
的取值范围．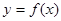
是定义域为
的奇函数，且当
时，
，（
。
的值；并求函数
上是增函数。
.
在点（1，
）处的切线方程；
在[1，2]上是减函数，求实数a的取值范围；
是否存在实数a，当
是自然对数的底）时，函数
的最小值是3，若存在，求出a的值；若不存在，说明理由.
.
，求
的单调区间及
,求
与
的大小
,并证明你的结论.
是奇函数，且当
时，
，求
时，
（m为常数0＜m＜1），且数列{f（
）}是首项为2，公差为2的等差数列．
＝
时，求数列｛
；
＝
，如果｛
，
（其中
）．
的极值；
在区间
内有两个零点，求正实数a的取值范围；（Ⅲ）求证：当
时，
．（说明：e是自然对数的底数，e=2.71828…）
的定义域为R，求实数m的取值范围.