题目内容
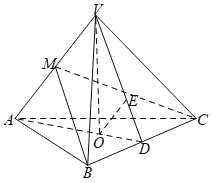
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,垂足
,垂足![]() 落在线段
落在线段![]() 上,
上,![]() 为
为![]() 的重心,已知
的重心,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)设点![]() 在线段
在线段![]() 上,使得
上,使得![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 为直二面角.
为直二面角.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)方法一:由重心的性质得出![]() ,再由
,再由![]() ,结合相似三角形的性质得出
,结合相似三角形的性质得出![]() ,再利用直线与平面平行的判定定理得出
,再利用直线与平面平行的判定定理得出![]() 平面
平面![]() ;
;
方法二:以![]() 为原点,以射线
为原点,以射线![]() 为
为![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]() ,利用重心的坐标公式计算出点
,利用重心的坐标公式计算出点![]() 的坐标,可计算出
的坐标,可计算出![]() ,可证明出
,可证明出![]() ,再利用直线与平面平行的判定定理得出
,再利用直线与平面平行的判定定理得出![]() 平面
平面![]() ;
;
(2)计算出![]() 和
和![]() ,利用向量的坐标运算计算出
,利用向量的坐标运算计算出![]() ,即可得出异面直线
,即可得出异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)由![]() ,得出
,得出![]() ,可求出
,可求出![]() 的坐标,然后可计算出平面
的坐标,然后可计算出平面![]() (即平面
(即平面![]() )的一个法向量
)的一个法向量![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() ,由题意得出
,由题意得出![]() ,结合空间向量数量积的坐标运算可求出实数
,结合空间向量数量积的坐标运算可求出实数![]() 的值.
的值.
(1)方法一:如图,连接![]() ,因为
,因为![]() 是
是![]() 的重心,
的重心,![]() 是
是![]() 的中点,
的中点,
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,又因为
,又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
方法二:以![]() 为原点,以射线
为原点,以射线![]() 为
为![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]() ,
,
则![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
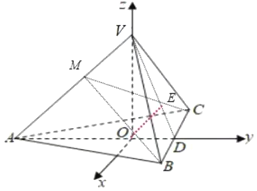
![]() 是
是![]() 的重心,则点
的重心,则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,
,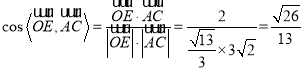 ,
,
所以异面直线![]() 与
与![]() 所成角的余弦值
所成角的余弦值![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
由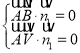 ,得
,得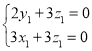 ,即
,即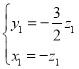 ,令
,令![]() ,可得
,可得![]() ,
,![]() ,
,
所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由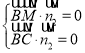 ,得
,得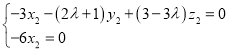 ,得
,得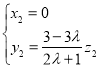 ,
,
取![]() ,则
,则![]() ,
,![]() ,
,
所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由于二面角![]() 为直二面角,所以,
为直二面角,所以,![]() ,
,
则![]() ,解得
,解得![]() ,合乎题意.
,合乎题意.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】某企业为打入国际市场,决定从![]() ,
,![]() 两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| 20 |
| 10 | 200 |
| 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关,![]() 为待定常数,其值由生产
为待定常数,其值由生产![]() 产品的原材料价格决定,预计
产品的原材料价格决定,预计![]() .另外,年销售
.另外,年销售![]() 件
件![]() 产品时需上交
产品时需上交![]() 万美元的特别关税.假设生产出来的产品都能在当年销售出去.
万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(1)写出该厂分别投资生产![]() ,
,![]() 两种产品的年利润
两种产品的年利润![]() 、
、![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系,并指明其定义域;
之间的函数关系,并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
