题目内容
设△ABC的内角A,B,C所对边的长分别为a,b,c,且有2sinBcosA=sinAcosC+cosAsinC.
(Ⅰ)求角A的大小;
(Ⅱ)若a=6,求△ABC的周长的取值范围.
(Ⅰ)求角A的大小;
(Ⅱ)若a=6,求△ABC的周长的取值范围.
考点:正弦定理的应用,三角函数中的恒等变换应用
专题:解三角形
分析:(Ⅰ)根据三角函数和角公式,得到2sinBcosA=sin(A+C),然后,结合三角函数中角的关系,得到角A的大小;
(Ⅱ)结合(Ⅰ),正弦定理,得到b=4
sinB,c=4
sinC,然后,构造三角形的周长表达式,利用辅助角公式化简后,并且结合角度的范围,求解△ABC的周长的取值范围.
(Ⅱ)结合(Ⅰ),正弦定理,得到b=4
| 3 |
| 3 |
解答:
解:(Ⅰ)由三角函数的和角公式,得
2sinBcosA=sin(A+C),
∵B=π-(A+C),
∴sinB=sin(A+C),
∴2sinBcosA=sinB,B∈(0,π),
∵sinB≠0,
∴2cosA=1,∵A∈(0,π),
∴A=
.
(Ⅱ)根据正弦定理,得
=
=
,
∵a=6,A=
,
b=4
sinB,c=4
sinC,B=
-C,
∴l=a+b+c
=6+4
sinB+4
sinC
=6+4
sin(
-C)+4
sinC
=6+6cosC+6
sinC
=6+12sin(C+
)
∵C∈(0,
),
∴C+
∈(
,
),
∴12sin(C+
)∈(6,12],
∴△ABC的周长的取值范围(12,18].
2sinBcosA=sin(A+C),
∵B=π-(A+C),
∴sinB=sin(A+C),
∴2sinBcosA=sinB,B∈(0,π),
∵sinB≠0,
∴2cosA=1,∵A∈(0,π),
∴A=
| π |
| 3 |
(Ⅱ)根据正弦定理,得
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∵a=6,A=
| π |
| 3 |
b=4
| 3 |
| 3 |
| 2π |
| 3 |
∴l=a+b+c
=6+4
| 3 |
| 3 |
=6+4
| 3 |
| 2π |
| 3 |
| 3 |
=6+6cosC+6
| 3 |
=6+12sin(C+
| π |
| 6 |
∵C∈(0,
| 2π |
| 3 |
∴C+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴12sin(C+
| π |
| 6 |
∴△ABC的周长的取值范围(12,18].
点评:本题综合考查了三角函数、三角恒等变换公式、解三角形等知识,属于中档题.

练习册系列答案
相关题目
设x,y满足
,则z=x-y( )
|
| A、有最小值2,无最大值 |
| B、有最小值-1,无最大值 |
| C、有最大值2,无最小值 |
| D、既无最小值,又无最大值 |
在区间[0,π]内随机取两个数分别记为a、b,则使得函数f(x)=x2+2ax-b2+π有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
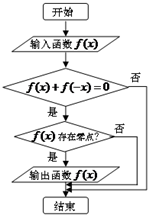

| A、f(x)=lnx | ||
B、f(x)=
| ||
| C、f(x)=ex | ||
| D、f(x)=x3 |