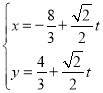题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为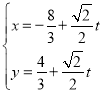 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
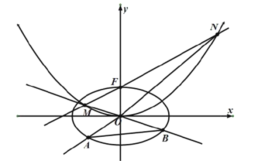
(Ⅱ)在平面直角坐标系![]() 中,设直线
中,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.若点
两点.若点![]() 恰为线段
恰为线段![]() 的三等分点,求
的三等分点,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;
;![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用消参法消去参数![]() ,即可将直线
,即可将直线![]() 的参数方程转化为普通方程,利用互化公式
的参数方程转化为普通方程,利用互化公式![]() ,
,![]() ,将曲线
,将曲线![]() 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(Ⅱ)把直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,得出关于
的直角坐标方程,得出关于![]() 的一元二次方程,根据韦达定理得出
的一元二次方程,根据韦达定理得出![]() 和
和![]() ,再利用直线参数方程中的参数
,再利用直线参数方程中的参数![]() 的几何意义,即可求出
的几何意义,即可求出![]() 的值.
的值.
解:(Ⅰ)由于直线![]() 的参数方程为
的参数方程为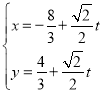 (
(![]() 为参数),
为参数),
消去参数![]() ,得直线
,得直线![]() 的普通方程为
的普通方程为![]() ,
,
由![]() ,
,![]() ,
,
得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,
的直角坐标方程,
并整理,得![]() ,
,![]()
设![]() ,
,![]() 是方程
是方程![]() 的两个根,则有
的两个根,则有![]() ,
,
得![]() ,
,![]() ,
,
由于点![]() 恰为线段
恰为线段![]() 的三等分点,
的三等分点,
所以不妨设![]() ,
,
∴![]() ,
,
解得:![]() ,符合条件
,符合条件![]() 和
和![]() ,
,
.∴![]() 的值为4.
的值为4.

练习册系列答案
相关题目
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中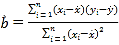 ,
,![]() .相关系数
.相关系数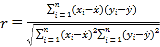 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()