若函数fx+1}{x}$+1为奇函数.则a=-1．题目和参考答案——青夏教育精英家教网—

题目内容

16．若函数f（x）=x+$\frac{（2a+1）x+1}{x}$+1为奇函数，则a=-1．

分析根据函数奇偶性的性质得到f（-x）=-f（x），从而得到关于a的方程，解出即可．

解答解：若函数$f（x）=x+\frac{（2a+1）x+1}{x}+1$为奇函数，
则f（-x）=-x-$\frac{1}{x}$+2a+1+1=-f（x）=-x-$\frac{1}{x}$-（2a+1）-1，
∴2（2a+1）+2=0，则a=-1，
故答案为：-1．

点评本题考查了函数奇偶性的性质，熟练掌握函数的性质是解题的关键，本题是一道基础题．

练习册系列答案

7．已知命题p：若平面α与平面β相交，则α内不存在与β平行的直线，命题q：若平面α与平面β不垂直，则α内不存在与β垂直的直线，那么下列复合命题中真命题的是（　　）

4．设函数f（x）=cosx•cos（x-θ）-$\frac{1}{2}$cosθ，θ∈（0，π）．已知当x=$\frac{π}{3}$时，f（x）取得最大值．
（1）求θ的值；
（2）设g（x）=2f（$\frac{3}{2}$x），求函数g（x）在[0，$\frac{π}{3}$]上的最大值．

11．已知扇形的周长为8cm，圆心角为2弧度，则该扇形的面积为4cm²．

1．已知a，b∈R，i是虚数单位，若a+i与2-bi互为共轭复数，则（a+bi）²=（　　）

8．已知复数$z=\frac{3+i}{1-i}$，则$|{\overline z}|$=（　　）

5．设x∈[0，2π]，利用单位圆解不等式sin（x+$\frac{π}{4}$）≥-$\frac{\sqrt{2}}{2}$可得x∈$\frac{3π}{2}$≤x≤$\frac{7π}{4}$或0≤x≤$\frac{π}{4}$．

6．

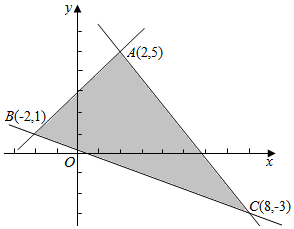直线l₁，l₂，l₃相交于A（2，5），B（-2，1），C（8，-3）．如图所示：
（1）用不等式组表示图中的阴影部分；
（2）设目标函数为z=3x-4y，图中的阴影部分是对x，y的约束条件，求在此约束条件下，目标函数的最大值和最小值；
（3）设目标函数为z=3x+4y，图中的阴影部分是对x，y的约束条件，求在此约束条件下，目标函数的最大值和最小值．

试题分类