Question

求证:两两相交且不共点的四条直线在同一平面内.

Answer 1

证明：如图14，直线a、b、c、d两两相交，交点分别为A、B、C、D、E、F,

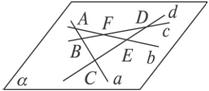
图14

∵直线a∩直线b=A,∴直线a和直线b确定平面设为α，即a,bα.

∵B、C∈a，E、F∈b,∴B、C、E、F∈α.

而B、F∈c，C、E∈d,∴c、dα,即a、b、c、d在同一平面内.

点评：在今后的学习中经常遇到证明点和直线共面问题，除公理2外，确定平面的依据还有：

(1)直线与直线外一点;(2)两条相交直线;(3)两条平行直线.