题目内容
设f(x)=ax2+bx,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
解析:方法一:设f(-2)=mf(-1)+nf(1)(m、n为待定系数),
则
即
所以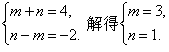
所以f(-2)=
因为1≤f(-1)≤2,2≤f(1)≤4,?
所以5≤
方法二:由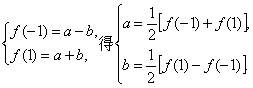
所以f(-2)=
因为1≤f(-1)≤2,2≤f(1)≤4,?
所以5≤
故5≤f(-2)≤10.

练习册系列答案
相关题目
题目内容
设f(x)=ax2+bx,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
解析:方法一:设f(-2)=mf(-1)+nf(1)(m、n为待定系数),
则
即
所以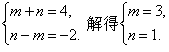
所以f(-2)=
因为1≤f(-1)≤2,2≤f(1)≤4,?
所以5≤
方法二:由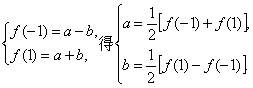
所以f(-2)=
因为1≤f(-1)≤2,2≤f(1)≤4,?
所以5≤
故5≤f(-2)≤10.
