题目内容
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(I)根据![]()
![]() ,设直线方程为
,设直线方程为![]() ,
,![]()
确定![]() 的坐标,由
的坐标,由![]() 确定得到
确定得到![]() ,
,
再根据![]() 点在椭圆上,求得
点在椭圆上,求得![]() 进一步即得所求
进一步即得所求![]() ;
;
(2)由![]() 可设
可设![]() ,
,
得到椭圆的方程为![]() ,
,
由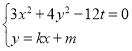 得
得![]()
根据动直线![]() 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
得到![]() ,整理得
,整理得![]() .
.
确定![]() 的坐标
的坐标![]() ,
,
又![]() ,
, ![]()
![]()
若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,那么
,那么![]()
可得![]() ,由
,由![]() 恒成立,故
恒成立,故![]() ,得解.
,得解.
试题解析:(1)∵![]()
![]() ,设直线方程为
,设直线方程为![]() ,
,![]()
令![]() ,则
,则![]() ,∴
,∴![]() , 2分
, 2分
∴![]() 3分
3分
∵![]() ,∴
,∴![]() =
=![]() ,
,
整理得![]() 4分
4分
∵![]() 点在椭圆上,∴
点在椭圆上,∴![]() ,∴
,∴![]() 5分
5分
∴![]() 即
即![]() ,∴
,∴![]() 6分
6分
(2)∵![]() 可设
可设![]() ,
,
∴椭圆的方程为![]() 7分
7分
由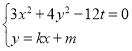 得
得![]() 8分
8分
∵动直线![]() 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
∴![]() ,即
,即![]()
整理得![]() 9分
9分
设![]()
![]() 则有
则有![]() ,
,![]()
∴![]() 10分
10分
又![]() ,
,![]()
![]()
若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,
,
∴![]() 恒成立
恒成立
整理得![]() , 12分
, 12分
∴![]() 恒成立,故
恒成立,故![]()
所求椭圆方程为![]() 13分
13分

【题目】我校举行的 “青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
组别 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0.16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0.40 |
第4组 | [80,90) | ▓ | 0.08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |
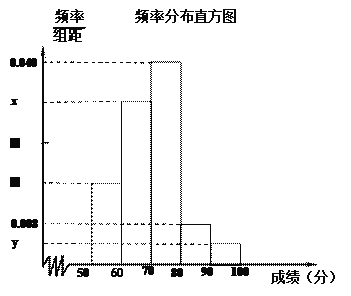
(1)求出![]() 的值;
的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;
(3)根据频率分布直方图,估计这50名学生成绩的众数、中位数和平均数。