题目内容
某三角形的三边长分别是2、3、4，则该三角形的面积是（ ）A．
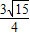
B．
C．
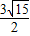
D．
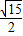
【答案】分析：利用余弦定理可求得最小角的余弦，进一步可求得其正弦值，从而可求得该三角形的面积．
解答：解：∵三角形的三边长分别是2、3、4，设最小角为α，
则cosα=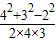
=
，
∴sinα=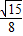
，
∴S△=
×3×4×
=
．
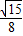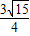故选A．
点评：本题考查余弦定理，求得最小角的余弦是基础，属于中档题．
解答：解：∵三角形的三边长分别是2、3、4，设最小角为α，
则cosα=
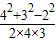=，∴sinα=
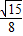，∴S△=
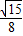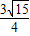×3×4×=．故选A．
点评：本题考查余弦定理，求得最小角的余弦是基础，属于中档题．
练习册系列答案
习题精选系列答案
相关题目
B． 
C．
D．
