【题目】如图，在平面直角坐标系中，有五个点，将二次函数的图象记为W．下列的判断中

①点A一定不在W上；

②点B，C，D可以同时在W上；

③点C，E不可能同时在W上．

所有正确结论的序号是_________．

观看直播课节数的频数分布表

其中，节数在这一组的数据是：

20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29

请根据所给信息，解答下列问题：

（1）__________，__________

（2）请补全频数分布直方图；

（3）随机抽取的50名学生观看直播课节数的中位数是___________；

（4）请估计该校学生中观看网络直播课节数不低于30次的约有__________人．

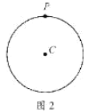
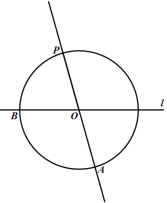
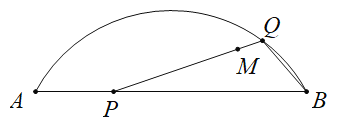
【题目】如图，M是弦与弧所围成的图形的内部的一个定点，P是弦上一动点，连接并延长交弧于点Q，连接．

已知，设A，P两点间的距离为，P，Q两点间距离为，两点间距离为．

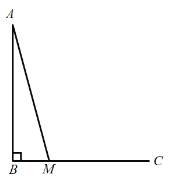
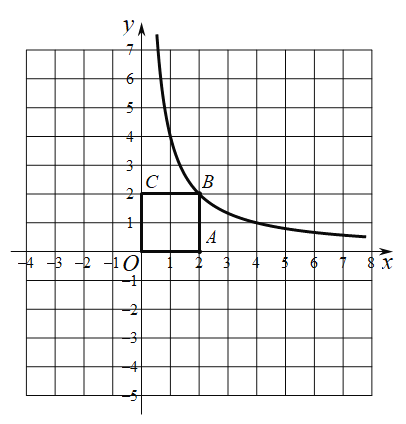
小明根据学习函数的经验，分别对函数随自变量x的变化而变化的规律进行了研究．下面是小明的探究过程，请补充完整．

（1）按照如表中自变量x的值进行取点、画图、测量，分别得到了与x的几组对应值，补全下表：

（2）在同一平面直角坐标系中，描出表中各组数值对应的点和并画出函数的图象；

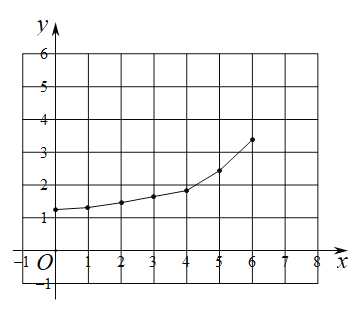
（3）结合函数图象，解决问题：当为等腰三角形时，的长度约_________．（精确到0.1）

【题目】在平面直角坐标系中，抛物线与x轴的交点为A，B，与y轴交于C．

（1）求抛物线的对称轴和点C坐标；

（2）横、纵坐标都是整数的点叫做整点．拋物线在点A，B之间的部分与线段所围成的区域为图形W（不含边界）．

①当时，求图形W内的整点个数；

②若图形W内有2个整数点，求m的取值范围．

【题目】如图，在中，，延长使，线段绕点C顺时针旋转90°得到线段，连结．

（1）依据题意补全图形；

（2）当时，的度数是__________；

（3）小聪通过画图、测量发现，当是一定度数时，．

小聪把这个猜想和同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

想法1：通过观察图形可以发现，如果把梯形补全成为正方形，就易证，因此易得当是特殊值时，问题得证；

想法2：要证，通过第（2）问，可知只需要证明是等边三角形，通过构造平行四边形，易证，通过，易证，从而解决问题；

想法3：通过，连结，易证，易得是等腰三角形，因此当是特殊值时，问题得证．

请你参考上面的想法，帮助小聪证明当是一定度数时，．（一种方法即可）

【题目】如图1，点P是平面内任意一点，点A，B是上不重合的两个点，连结．当时，我们称点P为的“关于的关联点”．

（1）如图2，当点P在上时，点P是的“关于的关联点”时，画出一个满足条件的，并直接写出的度数；

（2）在平面直角坐标系中有点，点M关于y轴的对称点为点N．

①以点O为圆心，为半径画，在y轴上存在一点P，使点P为“关于的关联点”，直接写出点P的坐标；

②点是x轴上一动点，当的半径为1时，线段上至少存在一点是的“关于某两个点的关联点”，求m的取值范围．

【题目】如图，在平面直角坐标系中，正方形的边长为2，函数的图象经过点B，与直线交于点D．

（1）求k的值；

（2）直线与边所在直线交于点M，与x轴交于点N．

①当点D为中点时，求b的值；

②当时，结合函数图象，直接写出b的取值范围．

已知：如图，直线l和直线外一点P．

求作：过点P作直线l的平行线．

作法：如图，

①在直线l上任取点O；

②作直线；

③以点O为圆心长为半径画圆，交直线于点A，交直线l于点B；

④连接，以点B为圆心，长为半径画弧，交于点C（点A与C不重合）；

⑤作直线．

则直线即为所求．

根据小元设计的尺规作图过程，完成以下任务．

（1）补全图形；

（2）完成下面的证明：

证明：连接

∵

∴

∴________________，

又∵，

∴________________，

∴，

∴（___________________________）（填推理的依据）．

假设所有粽子均能全部售出，则以下销售方式中利润最大的是____________．

方案一：不加工直接销售；

方案二：三天全部进行精加工，剩下的直接卖；

方案三：两天精加工，一天粗加工，剩下的直接卖；

方案四：两天粗加工，一天精加工，剩下的直接卖．

①甲和乙的动手操作能力都很强；

②缺少探索学习的能力是甲自身的不足；

③与甲相比乙需要加强与他人的沟通合作能力；

④乙的综合评分比甲要高．

其中合理的是（ ）

A.①③B.②④C.①②③D.①②③④