题目内容
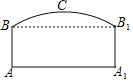
【题目】下面是小元设计的“过直线外一点作已知直线的平行线”的尺规作图过程.

已知:如图,直线l和直线外一点P.
求作:过点P作直线l的平行线.
作法:如图,
①在直线l上任取点O;
②作直线![]() ;
;
③以点O为圆心![]() 长为半径画圆,交直线
长为半径画圆,交直线![]() 于点A,交直线l于点B;
于点A,交直线l于点B;
④连接![]() ,以点B为圆心,
,以点B为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点C(点A与C不重合);
于点C(点A与C不重合);
⑤作直线![]() .
.
则直线![]() 即为所求.
即为所求.
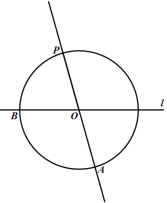
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:连接![]()
∵![]()
∴![]()
∴![]() _______
_______![]() _________,
_________,
又∵![]() ,
,
∴![]() _______
_______![]() _________,
_________,
∴![]() ,
,
∴![]() (___________________________)(填推理的依据).
(___________________________)(填推理的依据).
【答案】(1)详见解析;(2)CPB,APB;APB,OBP; 内错角相等,两直线平行.
【解析】
(1)根据作图第④步,第⑤步完成作图即可,(2)利用同圆中,等弧所对的圆周角相等及等腰三角形的性质可得答案.
解:(1)补全图形;

(2)证明:连接![]()
∵![]()
∴![]()
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (内错角相等两直线平行)
(内错角相等两直线平行)
故答案为:![]() 内错角相等,两直线平行.
内错角相等,两直线平行.

【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?
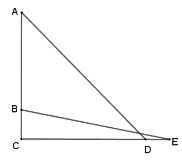
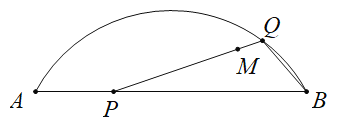
【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
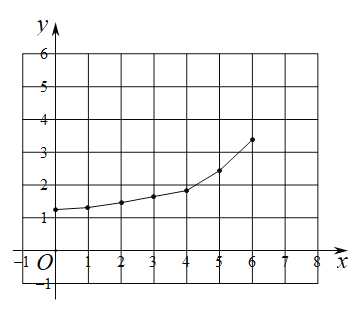
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)