【题目】为了鼓励城市周边的农民的种菜的积极性,某公司计划新建![]() ,
,![]() 两种温室80栋,将其售给农民种菜.已知建1个
两种温室80栋,将其售给农民种菜.已知建1个![]() 型温室和2个
型温室和2个![]() 型温室一共需要8.1万元,两种温室的成本和出售价如下表:
型温室一共需要8.1万元,两种温室的成本和出售价如下表:
|
| |
成本(万元/栋) | 2.5 |
|
出售价(万元/栋) | 3.1 | 3.5 |
(1)求![]() 的值;
的值;
(2)已知新建![]() 型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
【题目】勤俭节约一直是中华民族的传统美德,某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛,为此先对同学们每月零花钱的数额进行一些了解,随机调查了本校部分同学,根据调查结果绘制出了如下两个尚不完整的统计图表.
组别 | 分组(单位:元) | 人数 |
|
| 4 |
|
|
|
|
|
|
|
| 8 |
|
| 2 |
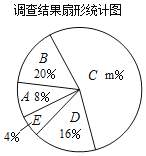
根据统计图表中的信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)扇形统计图中扇形![]() 的圆心角的度数为
的圆心角的度数为 ![]() ;所抽取同学零花钱的数额的中位数落在 范围;
;所抽取同学零花钱的数额的中位数落在 范围;
(3)该校共有1200名学生,请估计每月零花钱的数额在![]() 范围的人数.
范围的人数.
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?