0 327447 327455 327461 327465 327471 327473 327477 327483 327485 327491 327497 327501 327503 327507 327513 327515 327521 327525 327527 327531 327533 327537 327539 327541 327542 327543 327545 327546 327547 327549 327551 327555 327557 327561 327563 327567 327573 327575 327581 327585 327587 327591 327597 327603 327605 327611 327615 327617 327623 327627 327633 327641 366461


 =216(人),
=216(人), +400×
+400× +540×
+540× =604(人).
=604(人). ,
,

 BC=BD=CD,即可得出结论.
BC=BD=CD,即可得出结论. ,
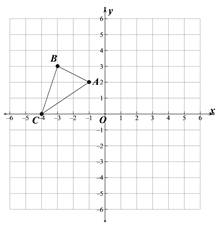
, (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD. AC时,求CE的长.
AC时,求CE的长.
 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD. AC时,求CE的长.
AC时,求CE的长.
 ;(2)
;(2) .
. (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积. AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长. (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2), ,即k=2.
,即k=2. .
. AC,∴BE=
AC,∴BE= .
. .∴点B的横坐标是
.∴点B的横坐标是 .
. .
. ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索: (其中
(其中
 .
. .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法. ,用含m、n的式子分别表示
,用含m、n的式子分别表示


 =( +
=( +  ,且
,且 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索: (其中
(其中
 .
. .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法. ,用含m、n的式子分别表示
,用含m、n的式子分别表示


 =( +
=( +  ,且
,且 ;
;
 ,
, 经过C、D两点.
经过C、D两点.

 ≤6的在数轴上表示为( )
≤6的在数轴上表示为( ) B.
B. 
 D.
D. 
 B.
B.  C.
C.  D.
D. 
 、
、 、
、 、
、 、
、 中,分式的个数有( )
中,分式的个数有( )