0 324837 324845 324851 324855 324861 324863 324867 324873 324875 324881 324887 324891 324893 324897 324903 324905 324911 324915 324917 324921 324923 324927 324929 324931 324932 324933 324935 324936 324937 324939 324941 324945 324947 324951 324953 324957 324963 324965 324971 324975 324977 324981 324987 324993 324995 325001 325005 325007 325013 325017 325023 325031 366461
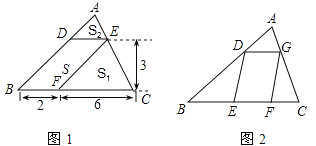
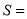 ______,△EFC的面积
______,△EFC的面积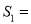 ______,△ADE的面积
______,△ADE的面积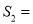 ______。
______。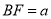 ,
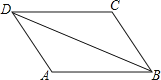
, 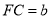 ,DE与BC间的距离为
,DE与BC间的距离为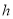 。请证明
。请证明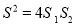 。
。
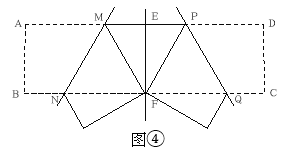
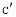 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么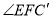 的度数为 。
的度数为 。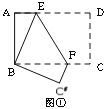
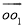 和
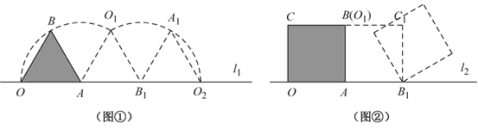
和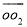 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形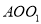 的面积、△AO1B1的面积和扇形B1O1O2的面积之和。
的面积、△AO1B1的面积和扇形B1O1O2的面积之和。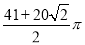 ?
?
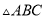 ≌
≌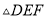 ,且△ABC的周长为20,AB=5,BC=8,则DF=( )
,且△ABC的周长为20,AB=5,BC=8,则DF=( )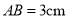 ,
, 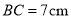 ,
, 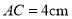 B.
B. 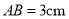 ,
, 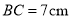 ,
, 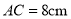
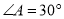 ,
, 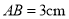 D.
D. 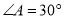 ,
, 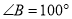 ,
, 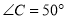
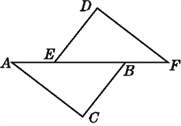
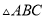 中,
中, 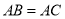 ,
, 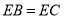 ,则由“
,则由“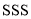 ”可判定( )
”可判定( )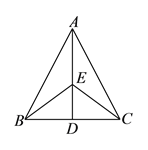
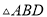 ≌
≌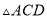 B.
B. 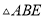 ≌
≌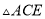 C.
C. 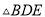 ≌
≌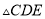 D. 以上答案都不对
D. 以上答案都不对