在△ABC中，AB=AC，AB的垂直平分线与AC所在的直线相交所得到锐角为50°，则∠B等于_____．
6种
【解析】试题分析：当△ABC是锐角三角形时，则∠B=70°，当△ABC是钝角三角形时，则∠B=20°. 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在( )
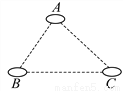
A. 在AC、BC两边高线的交点处 B. 在AC、BC两边中线的交点处
C. 在∠A、∠B两内角平分线的交点处 D. 在AC、BC两边垂直平分线的交点处
D
【解析】根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等可得：
超市应建在△ABC三条边的垂直平分线的交点处．
故选D． 如图，点D在BC上，DE⊥AB，DF⊥AC，垂足分别为E、F，DE＝DF.求证：AD垂直平分EF.
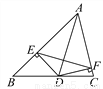
见解析
【解析】试题分析：根据直角三角形的判定定理证明Rt△AED≌Rt△AFD，得到AE=AF，根据线段垂直平分线的判定定理证明结论．
试题解析：
在Rt△AED和Rt△AFD中，
∴Rt△AED≌Rt△AFD（HL），
∴AE=AF，
又∵DE=DF，
∴AD是EF的垂直平分线，即AD垂直平分EF． 如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD垂直平分线与AB的交点，DE交AC于点F.求证：点E在AF的垂直平分线上．
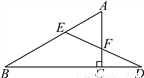
见解析
【解析】试题分析：过E作EG垂直于AC，交AC于G，可得出EG∥BD故∠AEG=∠B，∠D=∠DEG．再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D，根据ASA定理得出△AEG≌△FEG，进而可得出结论．
试题解析：
证明：如图所示：
过E作EG垂直于AC，交AC于G，
∵∠ACB=90°，
∴EG∥BD，
∴∠AEG=∠B，∠D=∠DEG．
∵... 如图，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F.若BF＝3cm.求BC.
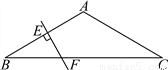
9cm
【解析】试题分析：先根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°，根据线段垂直平分线性质和等腰三角形性质求出∠BAF=30°，根据含30度角的直角三角形性质求出AF、FC即可．
试题解析：
∵在△ABC中，AB=AC，∠A=120°，
∴∠B=∠C=30°，
∵AB的垂直平分线EF，
∴AF=BF，
∴∠BAF=∠B=30°，
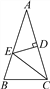
又∵BF=3... 如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.
求∠ECD的度数；
36°
【解析】试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE，然后根据等边对等角可得∠ECD=∠A；
试题解析：
∵ED垂直平分AC，
∴AE=CE，
∴∠ECD=∠A，
∵∠A=36°，
∴∠ECD=36°； 线段垂直平分线上的点到这条线段两个端点的距离____.
相等
【解析】根据线段垂直平分线的性质可得：线段垂直平分线上的点到这条线段两个端点的距离相等.
故答案是：相等. 如图，已知线段AB。
（1）用尺规作图的方法作出线段AB的垂直平分线l（保留作图痕迹，不要求写出作法）；
（2）在（1）中所作的直线l上任意取两点M、N（线段AB的上方），连接AM、AN。BM、BN。
求证：∠MAN=∠MBN。
【解析】
（1）作图如下：
（2）证明：根据题意作出图形如图，
∵点M、N在线段AB的垂直平分线l上，
∴AM=BM，AN=BN。
又 ∵MN=MN，∴△AMN≌△BMN（SSS）。
∴∠MAN=∠MBN。
【解析】（1）根据线段垂直平分线的性质作图。
（2）根据线段垂直平分线上的点到线段两端距离相等的性质，可得AM=BM，AN=BN。MN是公共边，从而... 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）
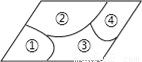
A. ①，② B. ①，④ C. ③，④ D. ②，③
D
【解析】分析：本题考查的是平行四边形的性质.
解析：破碎的玻璃中的②和③是连接的，可以得到四边形的大小.
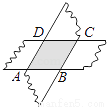
故选B. 如图，剪两张等宽对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是________．
菱形
【解析】试题分析：首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的等积转换可得邻边相等，则四边形ABCD为菱形．所以根据菱形的性质进行判断．
【解析】
过点D分别作AB，BC边上的高为AE，AF，
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形，
∴AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形（对边相互平行的四边...