一个直角三角形的两条直角边长分别为6 cm和8 cm，那么这个直角三角形的斜边长为（ ）
A. 6 cm B. 8 cm C. 10 cm D. 24 cm
C
【解析】根据勾股定理可以得出：斜边长==10cm.
故选：C． 如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC＝BC，则下列选项正确的是（ ）
A. 
B. 
C. 
D. 
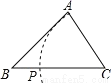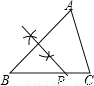
D
【解析】试题分析：由PB+PC=BC和PA+PC=BC易得PA=PB，根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上，于是可判断D选项正确．
故选D． 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）
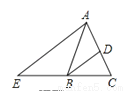
A. 40° B. 45° C. 60° D. 70°
A
【解析】根据平行线的性质可得∠CBD的度数，根据角平分线的性质可得∠CBA的度数，根据等腰三角形的性质可得∠C的度数，根据三角形内角和定理可得∠BAC的度数．
【解析】
∵AE∥BD，∴∠CBD=∠E=35°，∵BD平分∠ABC，∴∠CBA=70°，∵AB=AC，
∴∠C=∠CBA=70°，∴∠BAC=180°﹣70°×2=40°．
故选A．
“点睛”考查了平行... 如图，在△ABC中，AC＝4 cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7 cm，则BC的长为（ ）
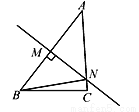
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
C
【解析】试题分析：根据中垂线的性质可得：BN=AN，则△BCN的周长=BN+NC+BC=AN+NC+BC=AC+BC=7cm，根据AC=4cm可得：BC=7－4=3cm. 下列命题中，其逆命题为真命题的是（ ）
A. 若a＝b，则a2＝b2 B. 同位角相等
C. 两边和一角对应相等的两个三角形全等 D. 等腰三角形两底角不相等
C
【解析】根据互为逆命题的关系，题设和结论互换，可知：
若a=b，则a2＝b2的逆命题为：若a2＝b2，则a=b，是假命题；
同位角相等的逆命题为：相等的角是同位角，是假命题；
两边和一角对应相等的两个三角形全等的逆命题是：全等三角形的对应边相等，对应角相等，是真命题；
等腰三角形的两底角不相等的逆命题为：两个角不相等的三角形是等腰三角形，是假命题.
故选：C... 如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB．若BE=2，则AE的长为（ ）
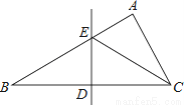
A.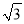 
B. 1 C. 
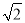D. 2
B
【解析】试题解析：∵在△ABC中，∠B=30°，BC的垂直平分线交AB于E，BE=2，
∴BE=CE=2，
∴∠B=∠DCE=30°，
∵CE平分∠ACB，
∴∠ACB=2∠DCE=60°，∠ACE=∠DCE=30°，
∴∠A=180°-∠B-∠ACB=90°．
在Rt△CAE中，∵∠A=90°，∠ACE=30°，CE=2，
∴AE=CE=1．
... 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
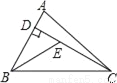
A. 10 B. 7 C. 5 D. 4
C
【解析】作EF⊥BC于F，
∵BE平分∠ABC，ED⊥AB，EF⊥BC，
∴EF=DE=2，
∴S△BCE=BC?EF=×5×2=5，
故选C. 如图，△ABC和△DCE都是边长为2的等边三角形，点B，C，E在同一条直线上，连接BD，则BD的长为（ ）
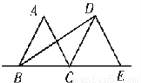
A. 18 B. 3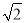
C. 12 D. 2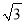
D
【解析】过点D作DF⊥EC于点F，利用正三角形的性质得出CF=1，BF=3，再利用勾股定理求出DF==，则可得BD=．
故选：D. 如图，在△ABC中，AB＝AC＝5，BC＝8，P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（ ）
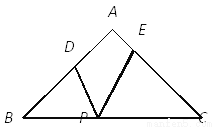
A. 4.8 B. 4.8或3.8 C. 3.8 D. 5
A
【解析】试题分析：作AF⊥BC于F，根据等腰三角形三线合一的性质得出BF=CF=4，然后根据勾股定理求得AF=3，连接AP，根据△ABC的面积=△ABP的面积+△ACP的面积解出答案即可. 命题“全等三角形的面积相等”的逆命题是 ．
面积相等的两个三角形全等
【解析】试题分析：把一个命题的题设和结论互换就可得到它的逆命题： “全等三角形的面积相等”的逆命题是：面积相等的三角形是全等三角形．