如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )

A. 8 B. 10 C. 12 D. 14
 B
【解析】试题分析:根据平行四边形的性质可知AB=CD,AD∥BC,AD=BC,然后根据平行线的性质和角平分线的性质可知AB=AF,DE=CD,因此可知AF+DE=AD+EF=2AB=12,解得AD=BC=12-2=10.
故选:B.
B
【解析】试题分析:根据平行四边形的性质可知AB=CD,AD∥BC,AD=BC,然后根据平行线的性质和角平分线的性质可知AB=AF,DE=CD,因此可知AF+DE=AD+EF=2AB=12,解得AD=BC=12-2=10.
故选:B. 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
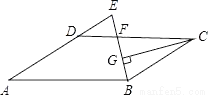
A. 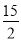 B.
B. 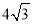 C.
C. 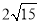 D.
D. 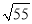
 C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2...
C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2... 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于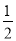 EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
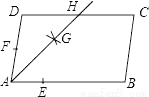
A. AG平分∠DAB B. AD=DH C. DH=BC D. CH=DH
 D
【解析】试题分析:由角平分线的作法,依题意可知AG平分∠DAB,A正确;∠DAH=∠BAH,又AB∥DC,所以∠BAH=∠ADH,所以,∠DAH=∠ADH,所以,AD=DH,又AD=BC,所以,DH=BC,B、C正确,故答案选D.
D
【解析】试题分析:由角平分线的作法,依题意可知AG平分∠DAB,A正确;∠DAH=∠BAH,又AB∥DC,所以∠BAH=∠ADH,所以,∠DAH=∠ADH,所以,AD=DH,又AD=BC,所以,DH=BC,B、C正确,故答案选D. 如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
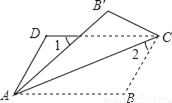
A. 66° B. 104° C. 114° D. 124°
 C
【解析】试题解析:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°;
故选C.
C
【解析】试题解析:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°;
故选C. 如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
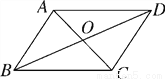
A. 10 B. 14 C. 20 D. 22
 B
【解析】试题分析:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,DC=AB=6,∵AC+BD=16,∴AO+BO=8,∴△ABO的周长是:14.故选B.
B
【解析】试题分析:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,DC=AB=6,∵AC+BD=16,∴AO+BO=8,∴△ABO的周长是:14.故选B. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A. 3种 B. 4种 C. 5种 D. 6种
 B
【解析】试题分析:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可...
B
【解析】试题分析:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可... 如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )
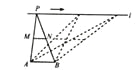
A. ②③ B. ②⑤ C. ①③④ D. ④⑤
 B
【解析】试题分析:
①、MN=AB,所以MN的长度不变;
②、周长C△PAB=(AB+PA+PB),变化;
③、面积S△PMN=S△PAB=×AB·h,其中h为直线l与AB之间的距离,不变;
④、直线NM与AB之间的距离等于直线l与AB之间的距离的一半,所以不变;
⑤、画出几个具体位置,观察图形,可知∠APB的大小在变化。
故选:B
B
【解析】试题分析:
①、MN=AB,所以MN的长度不变;
②、周长C△PAB=(AB+PA+PB),变化;
③、面积S△PMN=S△PAB=×AB·h,其中h为直线l与AB之间的距离,不变;
④、直线NM与AB之间的距离等于直线l与AB之间的距离的一半,所以不变;
⑤、画出几个具体位置,观察图形,可知∠APB的大小在变化。
故选:B 如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD=__.
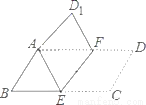
 55°.
【解析】试题分析:已知四边形ABCD是平行四边形,由平行四边形的性质可得∠BAD=∠C,再由折叠的性质得∠D1AE=∠C,所以∠D1AE=∠BAD,即可得∠D1AD=∠BAE=55°;
55°.
【解析】试题分析:已知四边形ABCD是平行四边形,由平行四边形的性质可得∠BAD=∠C,再由折叠的性质得∠D1AE=∠C,所以∠D1AE=∠BAD,即可得∠D1AD=∠BAE=55°; 如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.
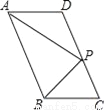
 24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD...
24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD... 如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________
(只添一个即可),使四边形ABCD是平行四边形
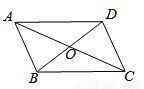
 BO=DO
【解析】【解析】
∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.故答案为:BO=DO.
BO=DO
【解析】【解析】
∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.故答案为:BO=DO.