题目内容
四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：
①AD∥BC；②AD=BC；③OA=OC；④OB=OD
从中任选两个条件，能使四边形ABCD为平行四边形的选法有（ ）
A. 3种 B. 4种 C. 5种 D. 6种
B
【解析】试题分析：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；
①③可证明△ADO≌△CBO，进而得到AD＝CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
①④可证明△ADO≌△CBO，进而得到AD＝CB，可...
全能测控期末小状元系列答案在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．
（1）求每台电脑、每台电子白板各多少万元？
（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．
（1）每台电脑0.5万元，每台电子白板1.5万元；（2）方案3最省钱，即购买电脑17台，电子白板13台最省
【解析】试题分析：（1）先设每台电脑x万元，每台电子白板y万元，根据购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元列出方程组，求出x，y的值即可；
（2）先设需购进电脑a台，则购进电子白板（30﹣a）台，根据需购进电脑和电子白板共30台，总费用... 如图，在?ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是_______．
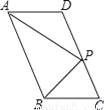
24
【解析】试题分析：∵四边形ABCD是平行四边形，
∴AD∥CB，AB∥CD，
∴∠DAB＋∠CBA＝180°，
又∵AP和BP分别平分∠DAB和∠CBA，
∴∠PAB＋∠PBA＝ (∠DAB＋∠CBA)＝90°，
在△APB中，∠APB＝180°－(∠PAB＋∠PBA)＝90°；
∵AP平分∠DAB，
∴∠DAP＝∠PAB，
∵AB∥CD... 如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
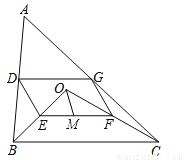
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
（1）证明见解析；（2）6．
【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
试题解析：（1）∵D、G分别是AB、AC的中点，... 如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为__．
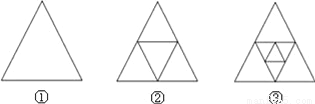
4n﹣3
【解析】试题解析：第①是1个三角形，1=4×1-3；
第②是5个三角形，5=4×2-3；
第③是9个三角形，9=4×3-3；
∴第n个图形中共有三角形的个数是4n-3 如图，在?ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，若AB＝6，EF＝2，则BC的长为( )
A. 8 B. 10 C. 12 D. 14
B
【解析】试题分析：根据平行四边形的性质可知AB=CD，AD∥BC，AD=BC，然后根据平行线的性质和角平分线的性质可知AB=AF，DE=CD，因此可知AF+DE=AD+EF=2AB=12，解得AD=BC=12-2=10.
故选：B. 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．
（1）求证：BM=MN；
（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．
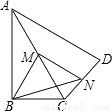
（1）证明见解析；（2）
【解析】试题分析：（1）在△CAD中，由中位线定理得到MN∥AD，且MN=AD，在Rt△ABC中，因为M是AC的中点，故BM=AC，即可得到结论；
（2）由∠BAD=60°且AC平分∠BAD，得到∠BAC=∠DAC=30°，由（1）知，BM=AC=AM=MC，得到∠BMC =60°．由平行线性质得到∠NMC=∠DAC=30°，故∠BMN90°，得到，再由MN=... 如图，?ABCD的对角线AC，BD相交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
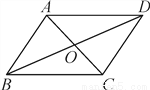
A. 13 B. 17 C. 20 D. 26
B
【解析】试题分析：由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
【解析】
∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B． 若函数y=mx²+(m+2)x+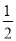
m+1的图象与x轴只有一个交点，那么m的值为( )
A. 0 B. 0或2 C. 2或－2 D. 0，2或－2
D
【解析】试题分析：当函数为一次函数时，则m=0；当函数为二次函数时，则，解得：m=±2.综上所述，m=0或2或－2.