某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )
A. 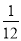 B.
B.  C.
C.  D.
D. 
 A
【解析】抬头看信号灯时,是黄灯的概率为:5÷(30+25+5)=5÷60= ,
故选:A.
A
【解析】抬头看信号灯时,是黄灯的概率为:5÷(30+25+5)=5÷60= ,
故选:A. 下列说法正确的是( )
A. 掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 某品牌电插座抽样检查的合格率为99%,说明即使购买1个该品牌的电插座,也可能不合格
C. “明天降雨的概率为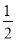 ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
 B
【解析】解:A.是随机事件,故A错误;
B.正确;
C.错误;
D.了解一批电视机的使用寿命,适合用抽样调查的方式,故D错误.
故选B.
B
【解析】解:A.是随机事件,故A错误;
B.正确;
C.错误;
D.了解一批电视机的使用寿命,适合用抽样调查的方式,故D错误.
故选B. 甲.乙.丙三个事件发生的概率分别为0.5,0.1,0.9,它们各与下面的哪句话相配.
(1)发生的可能性很大,但不一定发生;
(2)发生的可能性很小;
(3)发生与不发生的可能性一样.
 (1)发生的概率为0.9.
(2)发生的概率为0.1.
(3)发生的概率为0.5.
【解析】试题分析:
(1)概率比较大;
(2)概率比较小;
(3)概率为0.5.
试题解析:
(1)发生的可能性很大,但不一定发生,匹配发生的概率为0.9.
(2)发生的可能性很小,匹配发生的概率为0.1.
(3)发生与不发生的可能性一样,匹配发生的概率为...
(1)发生的概率为0.9.
(2)发生的概率为0.1.
(3)发生的概率为0.5.
【解析】试题分析:
(1)概率比较大;
(2)概率比较小;
(3)概率为0.5.
试题解析:
(1)发生的可能性很大,但不一定发生,匹配发生的概率为0.9.
(2)发生的可能性很小,匹配发生的概率为0.1.
(3)发生与不发生的可能性一样,匹配发生的概率为... 在一个不透明的袋中装有2个黄球,3个黑球和5个红球,它们除颜色外其他都相同.
(1)将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;
(2)现在再将若干个红球放入袋中,与原来的10个球均匀混合在一起,使从袋中随机摸出一个球是红球的概率是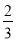 ,请求出后来放入袋中的红球的个数.
,请求出后来放入袋中的红球的个数.
 (1);(2)5
【解析】
试题分析:(1)用黄球的个数除以所有球的个数即可求得概率;
(2)根据概率公式列出方程求得红球的个数即可.
试题解析:(1)∵共10个球,有2个黄球,
∴P(黄球);
(2)设有x个红球,根据题意得:,解得:x=5.
故后来放入袋中的红球有5个.
(1);(2)5
【解析】
试题分析:(1)用黄球的个数除以所有球的个数即可求得概率;
(2)根据概率公式列出方程求得红球的个数即可.
试题解析:(1)∵共10个球,有2个黄球,
∴P(黄球);
(2)设有x个红球,根据题意得:,解得:x=5.
故后来放入袋中的红球有5个. 国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.

 (1)300;(2)补图见解析;(3)40%;(4)720人.
【解析】试题分析:(1)根据题意即可得到结论;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
试题解析:(1)60÷20%=300(人),
答:此次抽查的学生数为300人.
故答案为:3...
(1)300;(2)补图见解析;(3)40%;(4)720人.
【解析】试题分析:(1)根据题意即可得到结论;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
试题解析:(1)60÷20%=300(人),
答:此次抽查的学生数为300人.
故答案为:3... 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的可能性大小是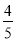 ,求m的值.
,求m的值.
 (1)填表见解析;(2)2.
【解析】试题分析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式列出方程,求得m的值即可.
试题解析:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(2)根据题意得: ,
解得:m=2,
所以m的...
(1)填表见解析;(2)2.
【解析】试题分析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式列出方程,求得m的值即可.
试题解析:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(2)根据题意得: ,
解得:m=2,
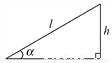
所以m的... 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,那么滑梯长l为( )
A. 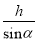 B.
B. 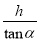 C.
C. 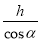 D. h·sinα
D. h·sinα
 A
【解析】根据锐角三角函数的定义可得,sinα= ,即可得l=,故选A.
A
【解析】根据锐角三角函数的定义可得,sinα= ,即可得l=,故选A. 如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于B,连AB,∠α=75°,则b值为( )
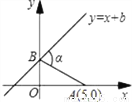
A. 3 B.  C. 4 D.
C. 4 D. 
 B
【解析】因为直线的解析式是y=x+b,
∴OB=OC=b,则∠BCA=45°;
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°;
而点A的坐标是(5,0),
∴OA=5,
在Rt△BAO中,∠BAC=30°,OA=5,
∴tan∠BAO=
∴BO=,即b=.
故选B.
B
【解析】因为直线的解析式是y=x+b,
∴OB=OC=b,则∠BCA=45°;
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°;
而点A的坐标是(5,0),
∴OA=5,
在Rt△BAO中,∠BAC=30°,OA=5,
∴tan∠BAO=
∴BO=,即b=.
故选B. 根据所给条件解直角三角形,结果不能确定的是( )
①已知一直角边及其对角;②已知两锐角;③已知斜边和一锐角;④已知一直角边和一斜边;⑤已知直角边和一锐角.
A. ②③ B. ②④ C. 只有② D. ②④⑤
 C
【解析】因为解直角三角形,至少已知条件中要给出一条边的长度,所以不能确定的只有②,故选C.
C
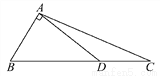
【解析】因为解直角三角形,至少已知条件中要给出一条边的长度,所以不能确定的只有②,故选C. 如图,在直角△BAD中,延长斜边BD到点C,使DC=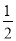 BD,连接AC,若tanB=
BD,连接AC,若tanB=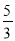 ,则tan∠CAD的值( )
,则tan∠CAD的值( )
A. 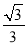 B.
B. 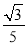 C.
C. 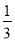 D.
D. 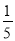
 D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.
D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.