点M(2，-3）与点N（2，3）关于______对称；点A(-2，-4）与点B（2，4）关于______对称；点G(4，0）与点H（-4，0）关于____________对称.
x轴 原点 y轴
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
所以点M与点N关于x轴对称,点A与点B关于原点对称,点G与点H关于y轴对称,故答案为: x轴, 原点, y轴. 直线y=x+3上有一点P(3，n)，则点P关于原点的对称点P′为________.
P′为（-3，-6）
【解析】因为直线y=x+3上有一点P（3,n）,所以n=3+3=6,所以P（3,6）,所以点P关于原点的对称点P′为（-3,-6）,故答案为:（-3,-6）. 已知点P(a，3)和P’(-4，b)关于原点对称，则(a+b)的值为__________.
1
【解析】因为点P(a,3)和P’(-4,b)关于原点对称,所以a+(－4)=0,3+b=0,所以a=4，b=－3,所以a+b=4+(－3)=1,故答案为:1. 已知点M(－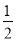
，3m)关于原点对称的点在第一象限，那么m的取值范围是____________.
m<0
【解析】因为点M（,3m）关于原点对称的点在第一象限,所以－3m＞0,所以m＜0,故答案为:m＜0. 如下图，利用关于原点对称的点的坐标的特点，作出与四边形ABCD关于原点对称的图形.
A、B、C、D关于原点对称的点的坐标分别为(2，－3)、(4，－1)、(3，1) (1，0)，图见解析.
【解析】因为关于原点的对称点,横纵坐标都变成相反数,的A,B,C,D关于原点对称的点的坐标分别为:A′（2,－3）,B′（4,－1）,C′（3,1）,D′（1,0）,如图所示:四边形A′B′C′D′即为所求. 直角坐标系中，已知点P(－2，－1)，点T(t，0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时，△P′TO是等腰三角形?
（1）点P关于原点的对称点P′的坐标为(2，1)；（2）综上所述，符合条件的t的值为－， ， ，4.
【解析】试题分析: （1）根据坐标关于原点对称的特点即可得出点P′的坐标,（2）要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原... 已知点A(2m，－3)与B(6，1－n)关于原点对称，求出m和n的值.
m＝－3，n＝－2.
【解析】试题分析:根据点关于原点对称的特征, 关于原点的对称点,横纵坐标都变成相反数,可得:2m+6=0,－3+1－n=0,解得: m=－3,n=－2.
试题解析:因为点A,B关于原点对称,所以,解得m=－3,n=－2. 如果点A(－3，2m+1)关于原点对称的点在第四象限，求m的取值范围.
m＞－
【解析】试题分析：由于第四象限关于原点对称的点在第二象限，反之第二象限的点关于原点对称的点在第四象限，所以A(－3,2m+1)应在第二象限，由第二象限的符号特征解之.
∵A(－3，2m+1)关于原点对称的点在第四象限.
∴A(－3，2m+1)在第二象限.
∴A点的纵坐标2m+1＞0.
∴m＞－. 求cos42°，下列按键正确的是( )
A. 
B. 
C. D. 
A
【解析】试题解析：用计算器计算一个锐角的三角函数值的步骤，先三角函数，之后度数，最后等号；
故选A. 用计算器求tanA＝0.5234时的锐角A(精确到1°)按键顺序正确的是( )
A. 
B. 
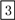
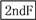
C.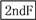
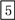
D.
C
【解析】试题解析：先按2ndF键，再按三角函数tan键，再依次输入0..5234，最后就可以出来答案．
故选C.