0 321093 321101 321107 321111 321117 321119 321123 321129 321131 321137 321143 321147 321149 321153 321159 321161 321167 321171 321173 321177 321179 321183 321185 321187 321188 321189 321191 321192 321193 321195 321197 321201 321203 321207 321209 321213 321219 321221 321227 321231 321233 321237 321243 321249 321251 321257 321261 321263 321269 321273 321279 321287 366461
 =0
=0
 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .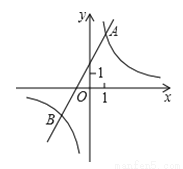
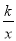 上,
上,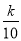 ,
,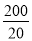 =10,
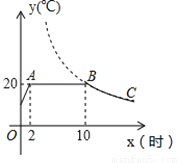
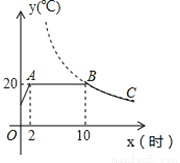
=10,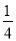 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.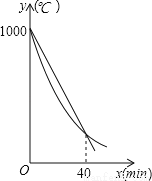
 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
 (x﹣60)2+m经过(0,1000),
(x﹣60)2+m经过(0,1000), (0﹣60)2+m,
(0﹣60)2+m, (x﹣60)2+100,
(x﹣60)2+100, ×(40﹣60)2+100,
×(40﹣60)2+100, ,
, ,
, (44﹣60)2+100=164(℃),
(44﹣60)2+100=164(℃), (x﹣60)2﹣100=﹣
(x﹣60)2﹣100=﹣ x2+10x=﹣
x2+10x=﹣ (x﹣20)2+100,
(x﹣20)2+100, cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
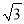 D.
D. 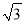

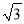 b C.
b C. 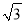 a D. 2a
a D. 2a