0 320691 320699 320705 320709 320715 320717 320721 320727 320729 320735 320741 320745 320747 320751 320757 320759 320765 320769 320771 320775 320777 320781 320783 320785 320786 320787 320789 320790 320791 320793 320795 320799 320801 320805 320807 320811 320817 320819 320825 320829 320831 320835 320841 320847 320849 320855 320859 320861 320867 320871 320877 320885 366461
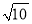 、
、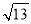 ;
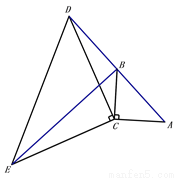
;
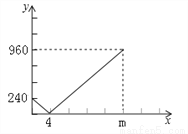
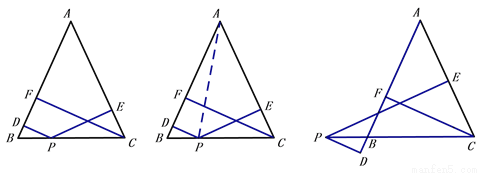
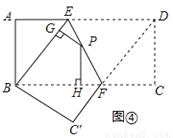
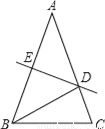
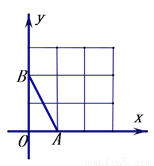
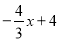 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
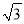 ,﹣1,0,3四个数中,最小的数为( )
,﹣1,0,3四个数中,最小的数为( )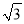 D. 3
D. 3
 B.
B.  C.
C.  D.
D.