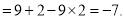题目内容
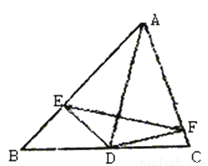
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
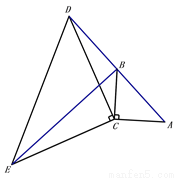
(1)求证:△ACD≌△BCE;
(2) 若AC=3cm,求BE的长度.
(1)详见解析;(2). 【解析】试题分析:(1)根据等腰直角三角形的性质得到然后利用“SAS”可判断≌即可; (2)根据全等三角形的性质得到即可; 试题解析:(1)证明:∵△CDE是等腰直角三角形, ∴CD=CE, ∴∠ACB=∠DCE, ∴∠ACB+∠BCD=∠DCE+∠BCD, ∴∠ACD=∠BCE, 在△ACD和△BCE中, ∴△ACD≌△...
练习册系列答案
相关题目


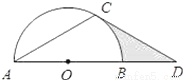
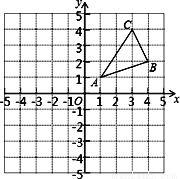
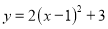 的顶点坐标是( )
的顶点坐标是( )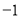 ,
, 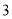 ) B. (
) B. (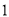 ,
, 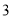 ) C. (
) C. (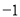 ,
, 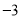 ) D. (
) D. (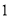 ,
, 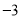 )
)
 B.
B.  C.
C.  D.
D. 
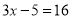 ; (2)
; (2) 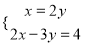
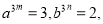 求
求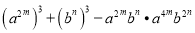 的值 。
的值 。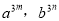 的形式,然后代入运算即可.
的形式,然后代入运算即可.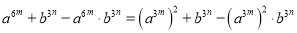 ,
,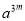 =3,
=3, 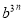 =2代入,
=2代入,