0 320521 320529 320535 320539 320545 320547 320551 320557 320559 320565 320571 320575 320577 320581 320587 320589 320595 320599 320601 320605 320607 320611 320613 320615 320616 320617 320619 320620 320621 320623 320625 320629 320631 320635 320637 320641 320647 320649 320655 320659 320661 320665 320671 320677 320679 320685 320689 320691 320697 320701 320707 320715 366461

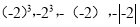 中,负数的个数是( )
中,负数的个数是( )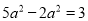 C.
C. 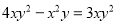 D.
D. 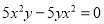
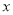 的方程
的方程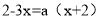 的解为x=-1,则a的值为( )
的解为x=-1,则a的值为( )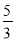
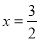
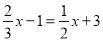 变形得4x﹣6=3x+18
变形得4x﹣6=3x+18