0 320183 320191 320197 320201 320207 320209 320213 320219 320221 320227 320233 320237 320239 320243 320249 320251 320257 320261 320263 320267 320269 320273 320275 320277 320278 320279 320281 320282 320283 320285 320287 320291 320293 320297 320299 320303 320309 320311 320317 320321 320323 320327 320333 320339 320341 320347 320351 320353 320359 320363 320369 320377 366461
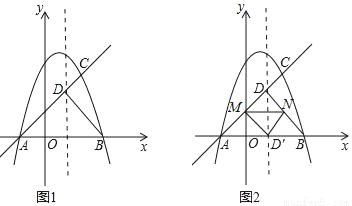
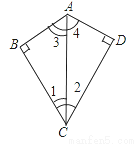
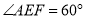 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.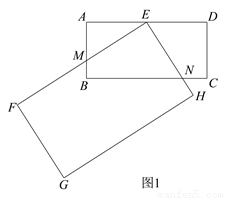

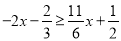 成立的最大的整数解是________.
成立的最大的整数解是________.