0 319329 319337 319343 319347 319353 319355 319359 319365 319367 319373 319379 319383 319385 319389 319395 319397 319403 319407 319409 319413 319415 319419 319421 319423 319424 319425 319427 319428 319429 319431 319433 319437 319439 319443 319445 319449 319455 319457 319463 319467 319469 319473 319479 319485 319487 319493 319497 319499 319505 319509 319515 319523 366461
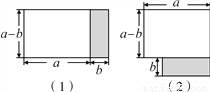
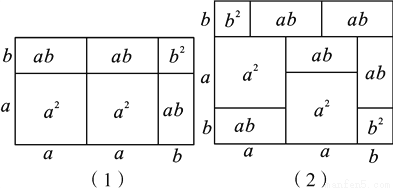
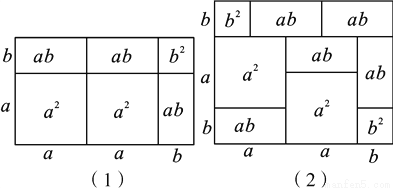
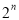
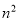
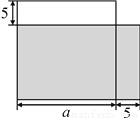

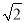 ;
;