��Ŀ����
��������ѧ�Ŀα��У�����ʽ�����ʽ��˿����ü���ͼ�ε��������ʾ.���磬��2a+b����a+b��=2a2+3ab+b2�Ϳ�����ͼ��1������ʾ.������ݴ˷���д��ͼ��2����ͼ�ε��������ʾ�Ĵ������ʽ��____________.
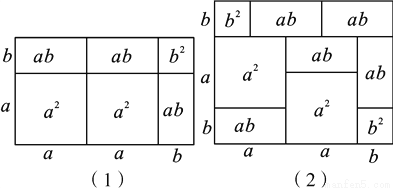
���𰸡���a+2b����2a+b��=2a2+5ab+2b2
�����������������ͼ�ڵ���������ó�Ϊa+a+b����Ϊb+a+b�ij�������������Ҳ�������ĸ���������5��С�����ε����֮���������ʾ�����ɣ�
��������
����ͼ���еã���a+2b����2a+b��=2a2+5ab+2b2��
�ʴ�Ϊ����a+2b����2a+b��=2a2+5ab+2b2��
���㣺����ʽ�˶���ʽ��
���������⿼���˶���ʽ���Զ���ʽ�����������շ����ǽⱾ��Ĺؼ���
�����͡������
��������
18
��һ���������ܱ�ʾΪ������������ƽ���������������Ϊ���ǻ���������3=22-12��16=52-32����3��16���ǻ�����.��֪����С�����˳���������У�3��5��7��8��9��11��12��13��15��16��17��19��20��21��23��24��25�������2 013�����ǻ�������______.
2 687 ���������������۲����ı仯���ɣ���֪ȫ�����ǻ�������С����ɰ�ÿ��������һ�飬�ӵ�2�鿪ʼÿ��ĵ�һ��������4�ı��������ɿɵã���n��ĵ�һ����Ϊ4n��n��2��.��Ϊ2 013��3=671�����Ե�2 013�����ǻ������ǵ�671���еĵ�3��������Ϊ4��671+3=2 687.
��ϰ��ϵ�д�
�����Ŀ


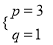 ����2��x2-2px+3q������ȫƽ��ʽ.���ɼ�����.
����2��x2-2px+3q������ȫƽ��ʽ.���ɼ�����.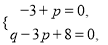
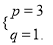
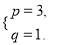 ����x2-2px+3q����x2-2px+3q=x2-6x+3.
����x2-2px+3q����x2-2px+3q=x2-6x+3.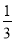 ��x��4��2���ɽ�������y=
��x��4��2���ɽ�������y=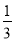 x2��������
x2��������