【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
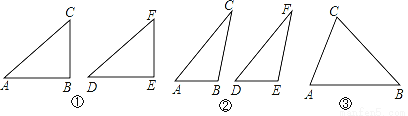
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.
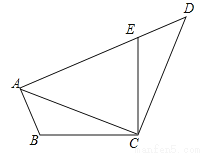
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.
将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
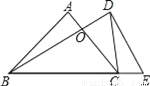
如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.
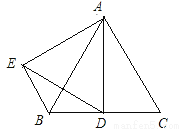
如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若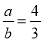 ,则
,则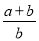 的值等于( ).
的值等于( ).
A. 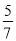 B.
B. 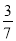 C.
C. 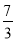 D.
D. 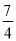
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.

如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.

将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.

如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若二次函数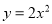 的图象经过点
的图象经过点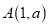 ,则
,则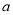 的值为( ).
的值为( ).
A. 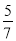 B.
B.  C.
C.  D.
D. 
若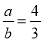 ,则
,则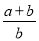 的值等于( ).
的值等于( ).
A. 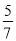 B.
B. 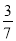 C.
C. 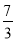 D.
D. 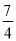
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.

如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.

将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
将抛物线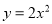 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 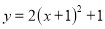 B.
B. 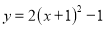 C.
C. 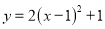 D.
D. 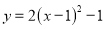
若二次函数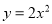 的图象经过点
的图象经过点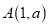 ,则
,则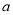 的值为( ).
的值为( ).
A. 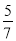 B.
B. 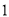 C.
C. 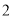 D.
D. 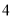
若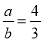 ,则
,则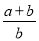 的值等于( ).
的值等于( ).
A. 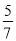 B.
B. 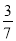 C.
C. 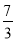 D.
D. 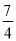
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.

如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图, 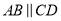 ,
, 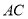 ,
, 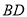 交于
交于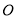 ,
, 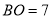 ,
, 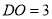 ,
, 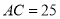 ,则
,则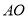 长为( ).
长为( ).
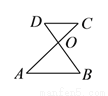
A. 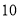 B.
B. 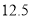 C.
C. 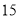 D.
D. 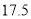
将抛物线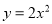 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 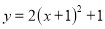 B.
B. 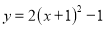 C.
C. 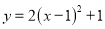 D.
D. 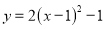
若二次函数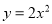 的图象经过点
的图象经过点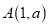 ,则
,则 的值为( ).
的值为( ).
A. 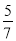 B.
B. 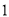 C.
C. 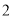 D.
D. 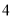
若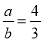 ,则
,则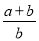 的值等于( ).
的值等于( ).
A. 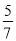 B.
B. 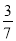 C.
C. 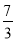 D.
D. 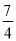
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.

如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
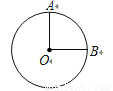
如图,已知 的半径
的半径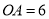 ,
, 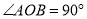 ,则
,则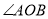 所对的弧
所对的弧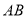 的长为( )
的长为( )
A. 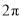 B.
B. 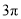 C.
C. 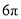 D.
D. 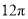
如图, 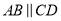 ,
, 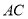 ,
, 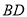 交于
交于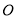 ,
, 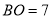 ,
, 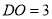 ,
, 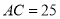 ,则
,则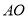 长为( ).
长为( ).
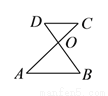
A. 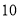 B.
B. 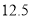 C.
C. 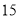 D.
D. 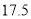
将抛物线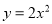 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 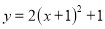 B.
B. 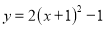 C.
C. 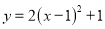 D.
D. 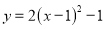
若二次函数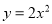 的图象经过点
的图象经过点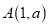 ,则
,则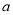 的值为( ).
的值为( ).
A. 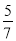 B.
B. 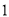 C.
C. 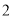 D.
D. 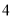
若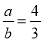 ,则
,则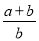 的值等于( ).
的值等于( ).
A. 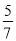 B.
B. 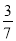 C.
C. 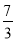 D.
D. 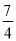
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在平面直角坐标系中,若⊙ 是以原点为圆心,
是以原点为圆心, 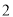 为半径的圆,则点
为半径的圆,则点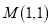 在( ).
在( ).
A. ⊙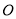 内 B. ⊙
内 B. ⊙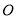 外 C. ⊙
外 C. ⊙ 上 D. 不能确定
上 D. 不能确定
如图,已知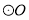 的半径
的半径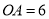 ,
, 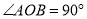 ,则
,则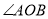 所对的弧
所对的弧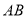 的长为( )
的长为( )

A. 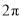 B.
B. 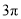 C.
C. 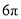 D.
D. 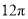
如图, 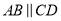 ,
, 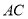 ,
, 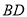 交于
交于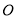 ,
, 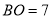 ,
, 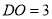 ,
, 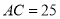 ,则
,则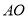 长为( ).
长为( ).
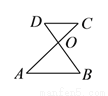
A. 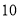 B.
B. 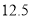 C.
C. 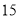 D.
D. 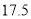
将抛物线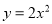 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 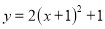 B.
B. 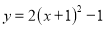 C.
C. 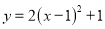 D.
D. 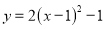
若二次函数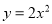 的图象经过点
的图象经过点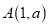 ,则
,则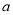 的值为( ).
的值为( ).
A. 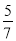 B.
B. 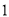 C.
C. 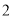 D.
D. 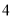
若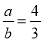 ,则
,则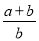 的值等于( ).
的值等于( ).
A. 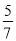 B.
B. 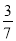 C.
C. 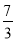 D.
D. 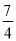
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,已知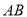 是⊙
是⊙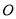 的直径,过点
的直径,过点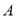 的弦
的弦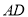 平行于半径
平行于半径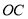 ,若
,若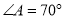 ,则
,则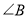 等于( ).
等于( ).

A. 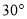 B.
B. 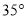 C.
C. 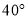 D.
D. 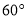
在平面直角坐标系中,若⊙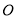 是以原点为圆心,
是以原点为圆心, 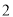 为半径的圆,则点
为半径的圆,则点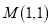 在( ).
在( ).
A. ⊙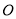 内 B. ⊙
内 B. ⊙ 外 C. ⊙
外 C. ⊙ 上 D. 不能确定
上 D. 不能确定
如图,已知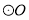 的半径
的半径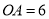 ,
, 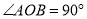 ,则
,则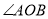 所对的弧
所对的弧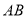 的长为( )
的长为( )

A. 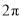 B.
B. 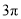 C.
C. 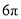 D.
D. 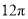
如图, 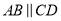 ,
, 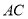 ,
, 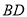 交于
交于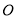 ,
, 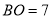 ,
, 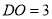 ,
, 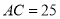 ,则
,则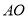 长为( ).
长为( ).
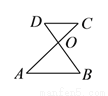
A. 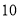 B.
B. 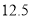 C.
C. 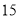 D.
D. 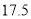
将抛物线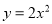 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 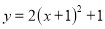 B.
B. 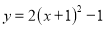 C.
C. 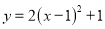 D.
D. 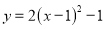
若二次函数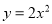 的图象经过点
的图象经过点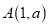 ,则
,则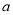 的值为( ).
的值为( ).
A. 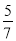 B.
B. 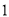 C.
C. 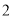 D.
D. 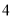
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
抛物线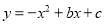 的部分图象如图所示,若
的部分图象如图所示,若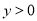 ,则
,则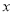 的取值范围是( ).
的取值范围是( ).
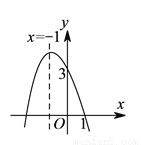
A. 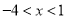 B.
B. 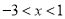 C.
C. 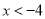 或
或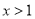 D.
D. 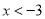 或
或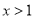
如图,已知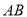 是⊙
是⊙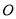 的直径,过点
的直径,过点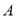 的弦
的弦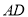 平行于半径
平行于半径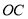 ,若
,若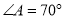 ,则
,则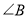 等于( ).
等于( ).

A. 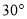 B.
B. 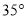 C.
C. 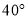 D.
D. 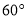
在平面直角坐标系中,若⊙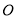 是以原点为圆心,
是以原点为圆心, 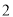 为半径的圆,则点
为半径的圆,则点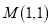 在( ).
在( ).
A. ⊙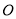 内 B. ⊙
内 B. ⊙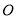 外 C. ⊙
外 C. ⊙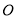 上 D. 不能确定
上 D. 不能确定
如图,已知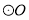 的半径
的半径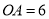 ,
, 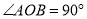 ,则
,则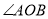 所对的弧
所对的弧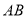 的长为( )
的长为( )

A. 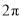 B.
B. 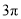 C.
C. 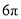 D.
D. 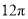
如图, 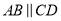 ,
, 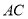 ,
, 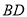 交于
交于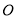 ,
, 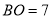 ,
, 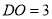 ,
, 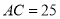 ,则
,则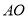 长为( ).
长为( ).
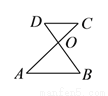
A. 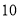 B.
B. 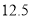 C.
C. 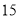 D.
D. 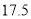
将抛物线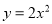 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 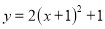 B.
B. 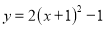 C.
C. 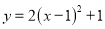 D.
D. 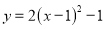
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
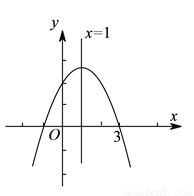
二次函数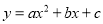 的图象,如图所示,有下列
的图象,如图所示,有下列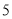 个结论:①
个结论:①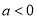 ;②
;②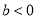 ;③
;③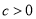 ;④
;④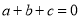 ;⑤
;⑤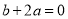 中,则其中正确的有( ).
中,则其中正确的有( ).
A. ①③④ B. ②④⑤ C. ①②④ D. ①③⑤
D 【解析】由函数图象可知:抛物线开口向下,∴a<0,故选项①正确; ∵对称轴在y轴右边,即x=?=1>0, 又a<0,∴b>0,故选项②错误; 又抛物线与y轴交点在y轴正半轴,∴c>0,故选项③正确; 当x=1时,对应的图象上的点在x轴上方,即y=ax2+bx+c=a+b+c>0,故选项④错误; 由x=?=1变形得:2a+b=0,故选项⑤正确; 综上,正...抛物线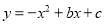 的部分图象如图所示,若
的部分图象如图所示,若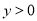 ,则
,则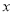 的取值范围是( ).
的取值范围是( ).

A. 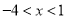 B.
B. 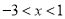 C.
C. 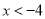 或
或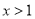 D.
D. 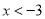 或
或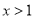
如图,已知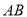 是⊙
是⊙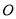 的直径,过点
的直径,过点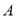 的弦
的弦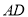 平行于半径
平行于半径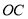 ,若
,若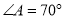 ,则
,则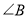 等于( ).
等于( ).

A. 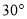 B.
B. 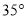 C.
C. 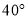 D.
D. 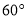
在平面直角坐标系中,若⊙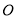 是以原点为圆心,
是以原点为圆心, 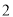 为半径的圆,则点
为半径的圆,则点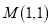 在( ).
在( ).
A. ⊙ 内 B. ⊙
内 B. ⊙ 外 C. ⊙
外 C. ⊙ 上 D. 不能确定
上 D. 不能确定
如图,已知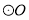 的半径
的半径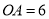 ,
, 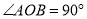 ,则
,则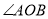 所对的弧
所对的弧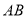 的长为( )
的长为( )

A. 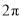 B.
B. 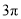 C.
C. 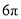 D.
D. 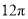
如图, 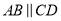 ,
, 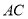 ,
, 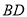 交于
交于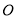 ,
, 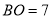 ,
, 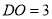 ,
, 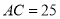 ,则
,则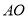 长为( ).
长为( ).
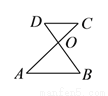
A. 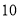 B.
B. 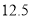 C.
C. 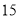 D.
D. 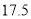
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧