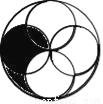
如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根，则代数式am2+bm﹣7的值为_____。
查看答案一组数据的方差为S2，将该数据每一个数据，都乘以4，所得到的一组新数据的方差是_________。
查看答案若圆锥的底面半径为3，母线长为6，则圆锥的侧面积等于_____．
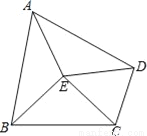
查看答案已知四边形ABCD内有一点E，满足EA=EB=EC=ED，且∠BCD=130°，那么∠BAD的度数为_____．
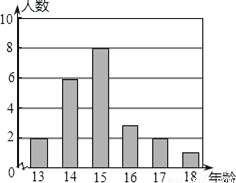
某校男子足球队队员的年龄分布为如图的条形图，则这些队员年龄的众数、中位数分别是_____。
- 题型：填空题
- 难度：困难
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
10﹪ 【解析】设每次下降的百分率为，根据题意可得： ， 解得（不合题意，舍去）， 所以每次下降的百分率为10%.如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根，则代数式am2+bm﹣7的值为_____。
查看答案一组数据的方差为S2，将该数据每一个数据，都乘以4，所得到的一组新数据的方差是_________。
查看答案若圆锥的底面半径为3，母线长为6，则圆锥的侧面积等于_____．
查看答案已知四边形ABCD内有一点E，满足EA=EB=EC=ED，且∠BCD=130°，那么∠BAD的度数为_____．
- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
不唯一如：（x+1）(x+2)=0 【解析】∵以为根，且二次项系数为1的一元二次方程为， ∴以-1，-2为根，且二次项系数为1的一元二次方程为，即.某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
查看答案如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根，则代数式am2+bm﹣7的值为_____。
查看答案一组数据的方差为S2，将该数据每一个数据，都乘以4，所得到的一组新数据的方差是_________。
查看答案若圆锥的底面半径为3，母线长为6，则圆锥的侧面积等于_____．
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
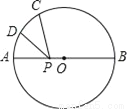
如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是
的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
查看答案某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
查看答案如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根，则代数式am2+bm﹣7的值为_____。
查看答案一组数据的方差为S2，将该数据每一个数据，都乘以4，所得到的一组新数据的方差是_________。
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
(1)x1=2，x2=;(2)x1=﹣3，x2=1 【解析】试题解析： （1）题选用“公式法”来解（也可用其它方法）； （2）题根据题目特点，选用“因式分解法”来解. 试题解析： （1）∵在方程中， ， ∴， ∴， ∴； （2）原方程可变形为： ， ∴或， 解得： .如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是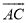的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
查看答案某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
查看答案如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根，则代数式am2+bm﹣7的值为_____。
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由.
（1）9，9（2）s2甲=；s2乙=；（3）甲，理由见解析. 【解析】试题分析：（1）首先根据图表得出甲、乙每一次的测试成绩，再利用平均数的计算公式分别求出甲、乙的平均成绩； （2）利用方差的计算公式即可求出甲、乙的方差； （3）结合方差的意义，从稳定性方面进行分析，即可得出结果． 【解析】 （1）=(10+8+9+8+10+9)÷6=9； =(10+7+10+10...解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
查看答案如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是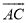的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
查看答案某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
查看答案如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
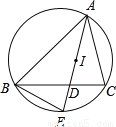
如图，点I是△ABC的内心，AI的延长线与边BC相交于点D，与△ABC的外接圆相交于点C．求证：IE=BE．
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由.
查看答案解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
查看答案如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是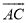的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
查看答案某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知关于x的一元二次方程x2－(2k＋1)x＋k2＋k＝0.
(1)求证：方程有两个不相等的实数根；
(2)若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为5，当△ABC是等腰三角形时，求k的值．
（1）证明见解析（2）k的值为5或4． 【解析】试题分析：（1）先计算出△=1，然后根据判别式的意义即可得到结论； （2）先利用公式法求出方程的解为x1=k，x2=k+1，然后分类讨论：AB=k，AC=k+1，当AB=BC或AC=BC时△ABC为等腰三角形，然后求出k的值． 试题解析：（1）证明：∵△=（2k+1）2﹣4（k2+k）=1＞0， ∴方程有两个不相等的实数根； ...如图，点I是△ABC的内心，AI的延长线与边BC相交于点D，与△ABC的外接圆相交于点C．求证：IE=BE．
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由.
查看答案解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
查看答案如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是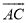的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
甲、乙两个不透明的口袋，甲口袋中装有3个分别标有数字1，2，3的小球，乙口袋中装有2个分别标有数字4，5的小球，它们的形状、大小完全相同，现随机从甲口袋中摸出一个小球记下数字，再从乙口袋中摸出一个小球记下数字．
（1）请用列表或树状图的方法（只选其中一种），表示出两次所得数字可能出现的所有结果；
（2）求出两个数字之和能被3整除的概率．
（1）树状图见解析；（2）. 【解析】试题分析：先根据题意画树状图，再根据所得结果计算两个数字之和能被3整除的概率． 试题解析：（1）树状图如下： （2）∵共6种情况，两个数字之和能被3整除的情况数有2种， ∴两个数字之和能被3整除的概率为， 即P（两个数字之和能被3整除）=．已知关于x的一元二次方程x2－(2k＋1)x＋k2＋k＝0.
(1)求证：方程有两个不相等的实数根；
(2)若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为5，当△ABC是等腰三角形时，求k的值．
查看答案如图，点I是△ABC的内心，AI的延长线与边BC相交于点D，与△ABC的外接圆相交于点C．求证：IE=BE．
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由.
查看答案解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
查看答案如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是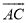的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某旅行社的一则广告如下：我社推出去井冈山红色旅游，收费标准为：如果组团人数不超过30人，人均收费800元；如果人数多于30人，那么每增加1人，人均收费降低10元，但人均收费不得低于500元，甲公司想分批组织员工到井冈山红色旅游学习．
（1）如果第一批组织38人去学习，则公司应向旅行社交费 元；
（2）如果公司计划用29250元组织第一批员工去学习，问这次旅游学习应安排多少人参加？
（1）27360；（2）应安排45人参加 【解析】试题分析： （1）由题意可列出式子：38×[800﹣（38﹣30）×10]计算可得结果； （2）首先由30×800=24000＜29250，可知这次去旅游的人数超过了30人， 设安排了人去旅游，由题意可列方程： ，解方程求得的值后，再由人均费用不低于500元进行检验即可得到答案. 试题解析： （1）∵人数多于30...甲、乙两个不透明的口袋，甲口袋中装有3个分别标有数字1，2，3的小球，乙口袋中装有2个分别标有数字4，5的小球，它们的形状、大小完全相同，现随机从甲口袋中摸出一个小球记下数字，再从乙口袋中摸出一个小球记下数字．
（1）请用列表或树状图的方法（只选其中一种），表示出两次所得数字可能出现的所有结果；
（2）求出两个数字之和能被3整除的概率．
查看答案已知关于x的一元二次方程x2－(2k＋1)x＋k2＋k＝0.
(1)求证：方程有两个不相等的实数根；
(2)若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为5，当△ABC是等腰三角形时，求k的值．
查看答案如图，点I是△ABC的内心，AI的延长线与边BC相交于点D，与△ABC的外接圆相交于点C．求证：IE=BE．
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由.
查看答案解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧